题目内容
已知点M(a,b)为直线y=-x+2
与双曲线y=
的交点.求:
(1)直线与x轴所成锐角的度数;
(2)|a2-b2|.
| 3 |
| 2 |
| x |
(1)直线与x轴所成锐角的度数;
(2)|a2-b2|.
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)利用直线平移得到线y=-x+2
是直线y=-x向上平移2
个单位得到,由此可判断直线与x轴所成锐角的度数;
(2)先解方程组方程组
可得到M点的坐标,即得到a与b的值,然后把a、b的值代入|a2-b2|中计算即可.
| 3 |
| 3 |
(2)先解方程组方程组
|
解答:解:(1)∵直线y=-x+2
是直线y=-x向上平移2
个单位得到,
∴直线与x轴所成锐角的度数为45°;
(2)∵方程组
的解为
或
,
∴M点的坐标为(
+1,
-1)或(
-1,
+1),
当a=
+1,b=
-1时,|a2-b2|=|(
+1)2-(
-1)2|=4
;
当a=
-1,b=
+1时,|a2-b2|=|(
-1)2-(
+1)2|=4
.
即|a2-b2|=4
.
| 3 |
| 3 |
∴直线与x轴所成锐角的度数为45°;
(2)∵方程组
|
|
|
∴M点的坐标为(
| 3 |
| 3 |
| 3 |
| 3 |
当a=
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
当a=
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
即|a2-b2|=4
| 3 |
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.

练习册系列答案
相关题目
抛物线y=2x2,y=-2x2,共有的性质是( )
| A、开口向下 |
| B、对称轴是y轴 |
| C、都有最低点 |
| D、y随x的增大而减小 |
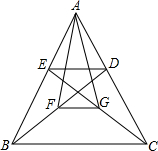 如图所示,一个△ABC,D是AC边上的一点,E是AB边上的一点,F是线段BD的中点,G是线段CE的中点,求△AFG的面积和四边形BCDE的面积比.
如图所示,一个△ABC,D是AC边上的一点,E是AB边上的一点,F是线段BD的中点,G是线段CE的中点,求△AFG的面积和四边形BCDE的面积比. 如图,△ABC中,∠BAC=54°,∠BAC的外角平分线交直线BC于D,若AB+AC=BD,求∠ABC的度数.
如图,△ABC中,∠BAC=54°,∠BAC的外角平分线交直线BC于D,若AB+AC=BD,求∠ABC的度数. 某菜农搭建一个横截面为抛物线的大棚,有关尺寸如图所示,若菜农身高为1.6米,则他在不弯腰的情况下在大棚里活动的范围是
某菜农搭建一个横截面为抛物线的大棚,有关尺寸如图所示,若菜农身高为1.6米,则他在不弯腰的情况下在大棚里活动的范围是