题目内容
3.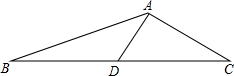 如图,在△ABC中,已知AB=13cm,AC=5cm,C边上的中线AD=6cm,求以BC为边长的正方形的面积.
如图,在△ABC中,已知AB=13cm,AC=5cm,C边上的中线AD=6cm,求以BC为边长的正方形的面积.
分析 延长AD至E,使ED=AD,连接BE,由中线的定义得出BD=CD=$\frac{1}{2}$BC,由SAS证明△BDE≌△CDA,得出对应边相等BE=AC=13,由勾股定理的逆定理证出∠BAD=90°,由勾股定理求出BD2,进一步求得BC2,即可得出结果.
解答 解:延长AD至E,使ED=AD,连接BE,如图所示: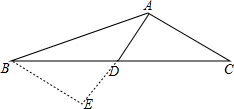
∵AD是BC边上的中线,
∴BD=CD=$\frac{1}{2}$BC,
在△BDE和△CDA中,
$\left\{\begin{array}{l}{ED=AD}\\{∠BDE=∠CDA}\\{BD=CD}\end{array}\right.$,
∴△BDE≌△CDA(SAS),
∴BE=AC=5(cm),
∵52+122=132,
∴BE2+AE2=AB2,
∴∠BED=90°,
∴BD2=AB2+AD2=52+62=61(cm2),
∴BC2=(2BD)2=4BD2=4×61=244(cm2).
点评 本题考查了全等三角形的判定与性质、勾股定理的逆定理、勾股定理;通过作辅助线构造三角形全等得出对应边相等证出直角三角形是解决问题的关键.

练习册系列答案
相关题目
13. 数a,b在数轴上的位置如图所示,则a-b是( )
数a,b在数轴上的位置如图所示,则a-b是( )
 数a,b在数轴上的位置如图所示,则a-b是( )
数a,b在数轴上的位置如图所示,则a-b是( )| A. | 正数 | B. | 零 | C. | 负数 | D. | 都有可能 |
18.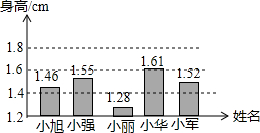 学习了统计图后,老师让小明按表提供的信息绘制统计图,小明绘制了如图所示的条形统计图.
学习了统计图后,老师让小明按表提供的信息绘制统计图,小明绘制了如图所示的条形统计图.
(1)小明绘制的统计图能反映每一位同学的身高吗?
(2)此图会使人产生错觉吗?应该怎样改动?
 学习了统计图后,老师让小明按表提供的信息绘制统计图,小明绘制了如图所示的条形统计图.
学习了统计图后,老师让小明按表提供的信息绘制统计图,小明绘制了如图所示的条形统计图.| 姓名 | 小旭 | 小强 | 小丽 | 小华 | 小军 |
| 身高/m | 1.46 | 1.55 | 1.28 | 1.61 | 1.52 |
(2)此图会使人产生错觉吗?应该怎样改动?
12.下列算式正确的是( )
| A. | ($\frac{a}{b}$)m=$\frac{{a}^{m}}{{b}^{m}}$ | B. | ($\frac{a+b}{b}$)2=$\frac{{a}^{2}+{b}^{2}}{{b}^{2}}$ | ||
| C. | (-$\frac{{y}^{3}}{{x}^{2}}$)2=-$\frac{{y}^{9}}{{x}^{4}}$ | D. | ($\frac{2x}{3y}$)4=$\frac{8{x}^{4}}{12{y}^{4}}$ |
13.某杂技团用68m长的幕布围成一个面积为300m2的矩形临时场地,并留出2m作为入口,则矩形场地的长为( )
| A. | 20m | B. | 15m | C. | 25m | D. | 30m |
 数a、b、c在数轴上对应的位置如图所示,化简|b-a|+|b-c|-|c|.
数a、b、c在数轴上对应的位置如图所示,化简|b-a|+|b-c|-|c|.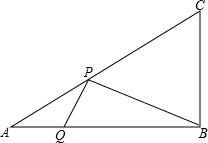 在△ABC中(AC>AB),∠A=30°,AB=2,P、Q分别为AC、AB上的点,求PB+PQ的最小值.
在△ABC中(AC>AB),∠A=30°,AB=2,P、Q分别为AC、AB上的点,求PB+PQ的最小值.