题目内容
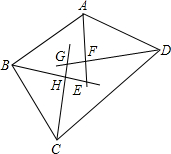 四边形ABCD的四个内角的平分线两两相交叉形成一个四边形EFGH,求证:
四边形ABCD的四个内角的平分线两两相交叉形成一个四边形EFGH,求证:(1)四边形EFGH对角互补;
(2)若四边形ABCD为平行四边形,则四边形EFGH为矩形;
(3)四边形ABCD为矩形,则四边形EFGH为正方形.
考点:正方形的判定,矩形的判定
专题:证明题
分析:(1)根据角平分线的定义可得∠EAB+∠EBA=
∠BAD+
∠ABC,∠GCD+∠GDC=
∠BCD+
∠ADC,然后根据四边形的内角和等于360°求出∠EAB+∠EBA+∠GCD+∠GDC=180°,再根据三角形的内角和定理列式求出∠E+∠G=180°,从而得证;
(2)根据平行四边形的邻角互补求出∠EAB+∠EBA=90°,再根据三角形的内角和定理求出∠E=90°,同理可求∠BHC=∠G=∠AFD=90°,然后根据四个角都是直角的四边形是矩形证明;
(3)判断出△ABE、△BCH、△CDG、△ADF都是等腰直角三角形,根据等腰直角三角形的性质求出AE=BE=CG=DG,BH=CH=AF=DF,然后求出EF=FG=GH=HE,再结合(2)证明即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据平行四边形的邻角互补求出∠EAB+∠EBA=90°,再根据三角形的内角和定理求出∠E=90°,同理可求∠BHC=∠G=∠AFD=90°,然后根据四个角都是直角的四边形是矩形证明;
(3)判断出△ABE、△BCH、△CDG、△ADF都是等腰直角三角形,根据等腰直角三角形的性质求出AE=BE=CG=DG,BH=CH=AF=DF,然后求出EF=FG=GH=HE,再结合(2)证明即可.
解答:(1)证明:∵四边形ABCD的四个内角的平分线两两相交,
∴∠EAB+∠EBA=
∠BAD+
∠ABC,∠GCD+∠GDC=
∠BCD+
∠ADC,
∵∠BAD+∠ABC+∠BCD+∠CDA=360°,
∴∠EAB+∠EBA+∠GCD+∠GDC=
×360°=180°,
∴∠E+∠G=180°-(∠EAB+∠EBA)+180°-(∠GCD+∠GDC)=180°,
同理可得∠BHC+∠AFD=180°,
∴∠EFG+∠EHG=180°,
故四边形EFGH对角互补;
(2)证明:∵四边形ABCD为平行四边形,
∴∠BAD+∠ABC=180°,
∴∠EAB+∠EBA=
∠BAD+
∠ABC=
×180°=90°,
∴∠E=180°-(∠EAB+∠EBA)=180°-90°=90°,
同理可得∠BHC=∠G=∠AFD=90°,
∴四边形EFGH为矩形;
(3)证明:∵四边形ABCD为矩形,四边形ABCD的四个内角的平分线两两相交,
∴△ABE、△BCH、△CDG、△ADF都是等腰直角三角形,
∴AE=BE=CG=DG,BH=CH=AF=DF,
∴EF=FG=GH=HE,
由(2)可知,四边形EFGH为矩形,
∴四边形EFGH为正方形.
∴∠EAB+∠EBA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BAD+∠ABC+∠BCD+∠CDA=360°,
∴∠EAB+∠EBA+∠GCD+∠GDC=
| 1 |
| 2 |
∴∠E+∠G=180°-(∠EAB+∠EBA)+180°-(∠GCD+∠GDC)=180°,
同理可得∠BHC+∠AFD=180°,
∴∠EFG+∠EHG=180°,
故四边形EFGH对角互补;
(2)证明:∵四边形ABCD为平行四边形,
∴∠BAD+∠ABC=180°,
∴∠EAB+∠EBA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠E=180°-(∠EAB+∠EBA)=180°-90°=90°,
同理可得∠BHC=∠G=∠AFD=90°,
∴四边形EFGH为矩形;
(3)证明:∵四边形ABCD为矩形,四边形ABCD的四个内角的平分线两两相交,
∴△ABE、△BCH、△CDG、△ADF都是等腰直角三角形,
∴AE=BE=CG=DG,BH=CH=AF=DF,
∴EF=FG=GH=HE,
由(2)可知,四边形EFGH为矩形,
∴四边形EFGH为正方形.
点评:本题考查了正方形的判定,矩形的判定,角平分线的定义,四边形的内角和定理,熟练掌握矩形,正方形与平行四边形的关系以及是解题的关键.

练习册系列答案
相关题目
如果a+
=1,b+
=2,那么c+
等于( )
| 2 |
| b |
| 2 |
| c |
| 1 |
| a |
| A、4 | B、3 | C、2 | D、1 |

 梯形ABCD中,AB∥DC,AD=BC,EB⊥DC,若BE=AB,DB=DC=10,求AB的长?
梯形ABCD中,AB∥DC,AD=BC,EB⊥DC,若BE=AB,DB=DC=10,求AB的长?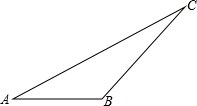 如图所示,已知在△ABC中,∠A=30°,∠B=135°,AC=8.求△ABC的面积.
如图所示,已知在△ABC中,∠A=30°,∠B=135°,AC=8.求△ABC的面积.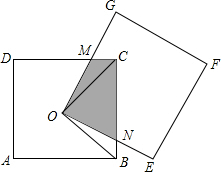 如图,正方形ABCD和正方形OEFG的边长均为4,O为正方形ABCD的中心.连接OG、OE分别与CD、BC交于M、N点,连接OC、OB.
如图,正方形ABCD和正方形OEFG的边长均为4,O为正方形ABCD的中心.连接OG、OE分别与CD、BC交于M、N点,连接OC、OB.