题目内容
11．
如图：在△ABC中，AB=AC，求证：∠B=∠C．
分析 作中线AD，根据三角形全等的判定定理证明△ABD≌△ACD，根据全等三角形的性质定理证明结论．
解答 证明：
作中线AD，
在△ABD和△ACD中，
$\left\{\begin{array}{l}{AB=AC}\\{BD=CD}\\{AD=AD}\end{array}\right.$，
∴△ABD≌△ACD，
∴∠B=∠C．
点评 本题考查的是三角形全等的判定和性质，掌握全等三角形的判定定理和性质定理是解题的关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
1．点A（m-3，m+1）在第二、四象限的平分线上，则A的坐标为（ ）
| A． | （-1，1） | B． | （-2，-2） | C． | （-2，2） | D． | （2，2） |
19．
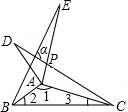如图，△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的，若∠BAC：∠ABC：∠BCA=28：5：3，则∠α的度数为（ ）
如图，△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的，若∠BAC：∠ABC：∠BCA=28：5：3，则∠α的度数为（ ）| A． | 90° | B． | 85° | C． | 80° | D． | 75° |
6．已知线段a，求作等边三角形ABC，使AB=a，作法如下：①作射线AM；②连结AC、BC；③分别以点A和点B为圆心，以a的长为半径作圆弧，两弧交于点C；④在射线AM上截取AB，使AB=a．其合理顺序为（ ）
| A． | ①②③④ | B． | ①④②③ | C． | ①④③② | D． | ②①④③ |
已知二次函数y=$\frac{1}{2}{x^2}$-3x+4．
如图，OD⊥BC，垂足为D，∠BOD=42°，求∠A的度数．
如图，点G是△ABC的重心，延长AG交BC于点F，GD∥BC，GD交AC于点D，若AD=6，求DC的长．
1．下列说法错误的是（ ）
| A． | $\sqrt{（-1）^{2}}$=1 | B． | $-\frac{\sqrt{5}}{5}$的倒数是-$\sqrt{5}$ | C． | 2的平方根是±$\sqrt{2}$ | D． | $\sqrt{（-3）×（-2）}$=$\sqrt{-3}$×$\sqrt{-2}$ |