题目内容
19.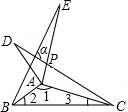 如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC:∠ABC:∠BCA=28:5:3,则∠α的度数为( )
如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC:∠ABC:∠BCA=28:5:3,则∠α的度数为( )| A. | 90° | B. | 85° | C. | 80° | D. | 75° |
分析 先根据三角形的内角和定理易计算出∠1=140°,∠2=25°,∠3=15°,根据折叠的性质得到∠1=∠BAE=140°,∠E=∠3=15°,∠ACD=∠E=15°,可计算出∠EAC,然后根据∠α+∠E=∠EAC+∠ACD,即可得到∠α=∠EAC.
解答 解:设∠3=3x,则∠1=28x,∠2=5x,
∵∠1+∠2+∠3=180°,
∴28x+5x+3x=180°,解得x=5°.
∴∠1=140°,∠2=25°,∠3=15°.
∵△ABE是△ABC沿着AB边翻折180°形成的,
∴∠1=∠BAE=140°,∠E=∠3=15°.
∴∠EAC=360°-∠BAE-∠BAC=360°-140°-140°=80°.
又∵△ADC是△ABC沿着AC边翻折180°形成的,
∴∠ACD=∠E=15°.
∵∠α+∠E=∠EAC+∠ACD,
∴∠α=∠EAC=80°.
故选:C.
点评 本题考查了折叠的性质:折叠前后两图形全等,即对应角相等,对应线段相等.也考查了三角形的内角和定理以及周角的定义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知等腰三角形的两条边长分别为4cm和9cm,则它的周长为( )
| A. | 17cm | B. | 22cm | C. | 9cm | D. | 17cm或22cm |
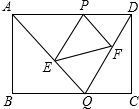 如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A,D),Q是BC边上的任意一点,连接AQ,DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.
如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A,D),Q是BC边上的任意一点,连接AQ,DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F. 如图:在△ABC中,AB=AC,求证:∠B=∠C.
如图:在△ABC中,AB=AC,求证:∠B=∠C.