题目内容
2.矩形的对角线长为8,两对角线的夹角为60°,则矩形的两邻边分别长4和4$\sqrt{3}$.分析 如图1, ,设两对角线的交点是E,作EF⊥CD于点F,判断出△CDE是等边三角形,即可求出CD的长度是多少;然后求出EF的长度,即可求出AD的长度是多少.
,设两对角线的交点是E,作EF⊥CD于点F,判断出△CDE是等边三角形,即可求出CD的长度是多少;然后求出EF的长度,即可求出AD的长度是多少.
解答 解:如图1,作EF⊥CD于点F, ,
,
∵四边形ABCD是矩形,
∴DE=CE=8÷2=4,
∵两对角线的夹角为60°,
∴∠CED=60°,
∴△CDE是等边三角形,
∴CD=DE=4;
又∵EF⊥CD于点F,
∴EF=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴AD=2EF=2×2$\sqrt{3}$=4$\sqrt{3}$,
综上,可得矩形的两邻边分别长4和4$\sqrt{3}$.
故答案为:4;$4\sqrt{3}$.
点评 此题主要考查了矩形的性质和应用,要熟练掌握,解答此题的关键是要明确矩形的性质:①平行四边形的性质矩形都具有;②角:矩形的四个角都是直角;③边:邻边垂直;④对角线:矩形的对角线相等;⑤矩形是轴对称图形,又是中心对称图形.它有2条对称轴,分别是每组对边中点连线所在的直线;对称中心是两条对角线的交点.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
12.“甲比乙少$\frac{2}{7}$”,应该把( )看作单位“1”.
| A. | 乙 | B. | 甲 | C. | $\frac{2}{7}$ | D. | 无法确定 |
10.已知等腰三角形的两条边长分别为4cm和9cm,则它的周长为( )
| A. | 17cm | B. | 22cm | C. | 9cm | D. | 17cm或22cm |
17.方程x(x+2)=3(x+2)的解是( )
| A. | 3和-2 | B. | 3 | C. | -2 | D. | 无解 |
12.函数y=kx+b的图象经过点(1,-1)且k:b=-3:4,则这个函数的表达式为( )
| A. | y=-3x+4 | B. | y=4x-5 | C. | y=3x-4 | D. | y=3x+4 |
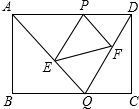 如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A,D),Q是BC边上的任意一点,连接AQ,DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.
如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A,D),Q是BC边上的任意一点,连接AQ,DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F. 如图:在△ABC中,AB=AC,求证:∠B=∠C.
如图:在△ABC中,AB=AC,求证:∠B=∠C.