题目内容
3.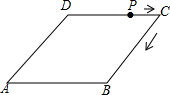 如图,菱形ABCD的边长为4,∠A=30°,点P从起点D出发,沿DC、CB向终点B匀速运动.设点P所走过的路程为x,△ADP的面积为y,则y关于x的函数图象是( )
如图,菱形ABCD的边长为4,∠A=30°,点P从起点D出发,沿DC、CB向终点B匀速运动.设点P所走过的路程为x,△ADP的面积为y,则y关于x的函数图象是( )| A. | 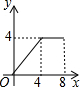 | B. | 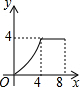 | C. | 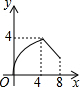 | D. | 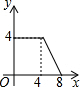 |
分析 根据题意可以得到点P在DC段和CB段对应的函数解析式,从而得到相应的三角形ADP的面积,本题得以解决.
解答 解:当点P从D到C的过程中,如下图所示,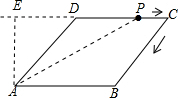
作AE⊥CD交CD的延长线于点E,
∴∠AED=90°,
∵AB∥CD,∠DAB=30°,AD=4,
∴∠EDA=30°,
∴AE=2,
∴${S}_{△ADP}=\frac{x•2}{2}=x$,
即y=x;
由C到B的过程中,
∵AD与BC之间的距离不变,
∴以AD当底边,点P到AD的距离不变,则三角形ADP的面积不变,
由上可得,函数图象正确是选项A,
故选A.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,求出各段对应的函数解析式,知道三角形的面积的求法.

练习册系列答案
相关题目
13.若m>n,下列不等式一定成立的是( )
| A. | m-2>n+2 | B. | 2m>2n | C. | -$\frac{m}{2}$>$\frac{n}{2}$ | D. | m2>n2 |
8.下面说法正确的是( )
| A. | 1的绝对值是-1 | B. | 1的倒数是-1 | C. | 1的相反数是-1 | D. | 1的平方根是-1 |
12.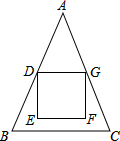 如图,小明把一个边长为10的正方形DEFG剪纸贴在△ABC纸片上,其中AB=AC=26,BC=20,正方形的顶点D,G分别在边AB、AC上,且AD=AG,点E、F在△ABC内部,则点E到BC的距离为( )
如图,小明把一个边长为10的正方形DEFG剪纸贴在△ABC纸片上,其中AB=AC=26,BC=20,正方形的顶点D,G分别在边AB、AC上,且AD=AG,点E、F在△ABC内部,则点E到BC的距离为( )
 如图,小明把一个边长为10的正方形DEFG剪纸贴在△ABC纸片上,其中AB=AC=26,BC=20,正方形的顶点D,G分别在边AB、AC上,且AD=AG,点E、F在△ABC内部,则点E到BC的距离为( )
如图,小明把一个边长为10的正方形DEFG剪纸贴在△ABC纸片上,其中AB=AC=26,BC=20,正方形的顶点D,G分别在边AB、AC上,且AD=AG,点E、F在△ABC内部,则点E到BC的距离为( )| A. | 1 | B. | 2 | C. | $\sqrt{21}$ | D. | $\sqrt{29}$ |
13.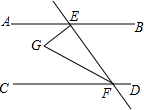 如图,AB∥CD,EF与AB,CD分别交于点E,F,EG⊥EF,与∠EFC的平分线FG交于点G.若∠EFG=25°,则∠AEG的大小为( )
如图,AB∥CD,EF与AB,CD分别交于点E,F,EG⊥EF,与∠EFC的平分线FG交于点G.若∠EFG=25°,则∠AEG的大小为( )
 如图,AB∥CD,EF与AB,CD分别交于点E,F,EG⊥EF,与∠EFC的平分线FG交于点G.若∠EFG=25°,则∠AEG的大小为( )
如图,AB∥CD,EF与AB,CD分别交于点E,F,EG⊥EF,与∠EFC的平分线FG交于点G.若∠EFG=25°,则∠AEG的大小为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
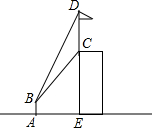 如图,为了测量某建筑物CE及建筑物上面的旗杆CD的高度(E,C,D三点在一条直线上),一测量员在距离建筑物底部E处10m的A处安置高为1.4m的测倾器AB,在B处测得旗杆顶部D的仰角为60°,旗杆底部C的仰角为45°,求建筑物CE及旗杆CD的高度(若运算结果有根号,保留根号).
如图,为了测量某建筑物CE及建筑物上面的旗杆CD的高度(E,C,D三点在一条直线上),一测量员在距离建筑物底部E处10m的A处安置高为1.4m的测倾器AB,在B处测得旗杆顶部D的仰角为60°,旗杆底部C的仰角为45°,求建筑物CE及旗杆CD的高度(若运算结果有根号,保留根号).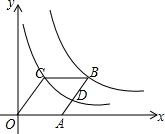 如图,菱形OABC中,∠AOC=45°,顶点B的坐标为(a,2),顶点A在x轴的正半轴上,反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过顶点B,y2=$\frac{{k}_{2}}{x}$(x>0)的图象经过顶点C,交AB于点D,以下结论:
如图,菱形OABC中,∠AOC=45°,顶点B的坐标为(a,2),顶点A在x轴的正半轴上,反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过顶点B,y2=$\frac{{k}_{2}}{x}$(x>0)的图象经过顶点C,交AB于点D,以下结论: