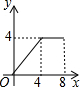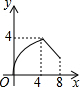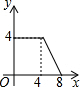题目内容
15.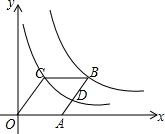 如图,菱形OABC中,∠AOC=45°,顶点B的坐标为(a,2),顶点A在x轴的正半轴上,反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过顶点B,y2=$\frac{{k}_{2}}{x}$(x>0)的图象经过顶点C,交AB于点D,以下结论:
如图,菱形OABC中,∠AOC=45°,顶点B的坐标为(a,2),顶点A在x轴的正半轴上,反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过顶点B,y2=$\frac{{k}_{2}}{x}$(x>0)的图象经过顶点C,交AB于点D,以下结论:(1)k1=4$\sqrt{2}+4$
(2)k2=4
(3)AD=BD
(4)S菱形OABC=4$\sqrt{2}$
其中正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 过点C作CE⊥x轴于点E,作BF⊥x轴于点F,由菱形的性质可知CE=OE=2,根据∠AOC=45°可知OE=CE,故可得出C点坐标,代入反比例函数解析式可得出k2的值;在Rt△OCE中,根据勾股定理求出OC的长,由菱形的性质可得出OA=OC,同理可得出B点坐标,进而得出k2的值;利用待定系数法求出直线AB的解析式,进而可得出D点坐标,求出AD及BD的长;直接根据菱形的面积公式即可得出菱形的面积.
解答 解:过点C作CE⊥x轴于点E,作BF⊥x轴于点F,
∵B(a,2),∠AOC=45°,
∴CE=OE=2.
∴C(2,2).
∵y2=$\frac{{k}_{2}}{x}$(x>0)的图象经过顶点C,
∴k2=2×2=4,故(2)正确;
在Rt△OCE中,
∵OE=CE=2,
∴OC=$\sqrt{{OE}^{2}+{CE}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$.
∵四边形OABC是菱形,
∴OA=OC=2$\sqrt{2}$,∠BAF=∠AOC=45°,
∴AF=BF=2,
∴B(2$\sqrt{2}$+2,2).
∵反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过顶点B,
∴k1=2(2$\sqrt{2}$+2)=4$\sqrt{2}$+4,故(1)正确;
设直线AB的解析式为y=kx+b(k≠0),
∵(2$\sqrt{2}$,0),B(2$\sqrt{2}$+2,2),
∴$\left\{\begin{array}{l}2\sqrt{2}k+b=0\\(2\sqrt{2}+2)k+b=2\end{array}\right.$,解得$\left\{\begin{array}{l}k=1\\ b=-2\sqrt{2}\end{array}\right.$,
∴直线AB的解析式为y=x-2$\sqrt{2}$,
∴$\left\{\begin{array}{l}y=\frac{4}{x}\\ y=x-2\sqrt{2}\end{array}\right.$,解得$\left\{\begin{array}{l}x=2+\sqrt{2}\\ y=2-\sqrt{2}\end{array}\right.$或$\left\{\begin{array}{l}x=2-\sqrt{2}\\ y=2-3\sqrt{2}\end{array}\right.$(舍去),
∴D(2+$\sqrt{2}$,2-$\sqrt{2}$).
∵A(2$\sqrt{2}$,0),B(2$\sqrt{2}$+2,2),
∴AD2=(2$\sqrt{2}$-2-$\sqrt{2}$)2+(2-$\sqrt{2}$)2=12-8$\sqrt{2}$,BD2=(2$\sqrt{2}$+2-2-$\sqrt{2}$)2+(2-2+$\sqrt{2}$)2=4,
∴AD≠BD,故(3)错误;
∵OA=2$\sqrt{2}$,CE=2,
∴S菱形OABC=OA•CE=2$\sqrt{2}$×2=4$\sqrt{2}$,故(4)正确.
∴(1)、(2)、(4)正确.
故选C.
点评 本题考查的是反比例函数综合题,涉及到反比例函数图象上点的坐标特点、菱形的性质等知识,根据题意作出辅助线,构造出等腰直角三角形是解答此题的关键.

| A. | $\frac{1}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{7}{6}$ | D. | 6 |
| A. | 1.7×104 | B. | 1.7×108 | C. | 1.7×1012 | D. | 1.7×1013 |
 小明帮助做生意的父亲整理仓库,在仓库的一角整齐地堆放着若干个相同的正方体货箱,如图是小明画出的这堆货箱的三种视图,这堆正方体货箱共有( )
小明帮助做生意的父亲整理仓库,在仓库的一角整齐地堆放着若干个相同的正方体货箱,如图是小明画出的这堆货箱的三种视图,这堆正方体货箱共有( )| A. | 11箱 | B. | 10箱 | C. | 9箱 | D. | 8箱 |
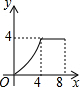
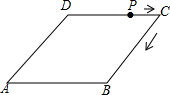 如图,菱形ABCD的边长为4,∠A=30°,点P从起点D出发,沿DC、CB向终点B匀速运动.设点P所走过的路程为x,△ADP的面积为y,则y关于x的函数图象是( )
如图,菱形ABCD的边长为4,∠A=30°,点P从起点D出发,沿DC、CB向终点B匀速运动.设点P所走过的路程为x,△ADP的面积为y,则y关于x的函数图象是( )