题目内容
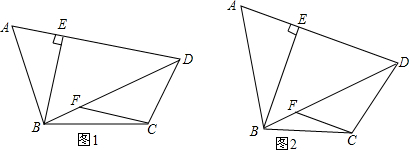
3.如图1,四边形ABCD中,AB=BC,BE⊥AD,垂足为E,∠BCD-ABE=90°,过点C作CF∥AD,交对角线BD于点F.(1)求证:CF=CD;
(2)若将“AB=BC”改为“AB=k•BC(k为常数,且k>0)”,其它条件不变(如图2),求$\frac{CF}{CD}$的值(用含k的式子表示).
分析 (1)过B作BQ⊥DC于Q,求出∠Q=∠BEA=90°,∠ABE=∠CBQ,根据AAS推出△BEA≌△BQC,求出BE=BQ,根据角平分线性质得出∠ADB=∠CDB,推出∠CFD=∠CDF即可;
(2)过B作BQ⊥DC交DC的延长线于H,连接AC,由BE⊥AD,得到∠ABE=90°-∠A,由于∠BCD-∠ABE=90°,于是得到∠BCD=90°+∠ABE=180°-∠A=180°-∠BCH,得到∠BCH=∠A,推出A,B,C,D四点共圆,于是得到∠BAC=∠CDF,∠ACB=∠ADB,证得△ABC~△DCF,即可得到结果.
解答 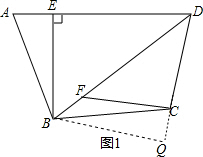 (1)证明:过B作BQ⊥DC于Q,
(1)证明:过B作BQ⊥DC于Q,
∵BE⊥AD,
∴∠Q=∠BEA=90°,
∴∠BCD-90°=∠QBC,
∵∠BCD-∠ABE=90°,
∴∠ABE=∠CBQ,
在△BEA和△BQC中,
$\left\{\begin{array}{l}{∠ABE=∠CBQ}\\{∠BEA=∠Q}\\{AB=BC}\end{array}\right.$,
∴△BEA≌△BQC(AAS),
∴BE=BQ,
∵BE⊥AD,BQ⊥DC,
∴∠ADB=∠CDB,
∵CF∥AD,
∴∠CFD=∠ADB,
∴∠CFD=∠CDF,
∴CF=CD;
(2)解:过B作BQ⊥DC交DC的延长线于H,连接AC,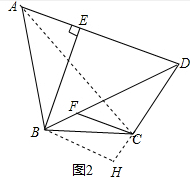
∵BE⊥AD,
∴∠ABE=90°-∠A,
∵∠BCD-∠ABE=90°,
∴∠BCD=90°+∠ABE=180°-∠A=180°-∠BCH,
∴∠BCH=∠A,∴A,B,C,D四点共圆,
∴∠BAC=∠CDF,∠ACB=∠ADB,
∵CF∥AD,
∴∠CFD=∠ADB=∠ACB,
∴△ABC~△DCF,
∴$\frac{CF}{CD}=\frac{BC}{AB}=\frac{BC}{k•BC}=\frac{1}{k}$.
点评 本题考查了全等三角形的性质和判定,角平分线性质,平行线性质,等腰三角形的判定的应用,解此题的关键是推出∠ADB=∠CDB,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等,

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | $\sqrt{{x}^{2}+1}=0$ | B. | $\sqrt{x-2}+\frac{1}{2}=0$ | C. | $\sqrt{x+1}=2$ | D. | $\sqrt{x-1}+\sqrt{1-x}=2$ |
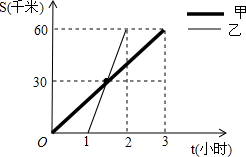 甲、乙两车分别从A地将一批物资运往B地,两车离A地的距离s(千米)与其相关的时间t(小时)变化的图象如图所示.读图后填空:
甲、乙两车分别从A地将一批物资运往B地,两车离A地的距离s(千米)与其相关的时间t(小时)变化的图象如图所示.读图后填空: 如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A-C路径向终点C运动;点Q从B点出发沿B-C-A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.则点P运动时间为1或$\frac{7}{2}$时,△PEC与△QFC全等.
如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A-C路径向终点C运动;点Q从B点出发沿B-C-A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.则点P运动时间为1或$\frac{7}{2}$时,△PEC与△QFC全等.