题目内容
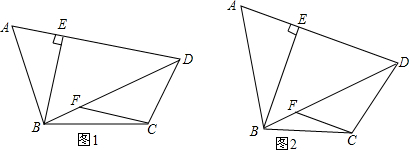
18. 如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A-C路径向终点C运动;点Q从B点出发沿B-C-A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.则点P运动时间为1或$\frac{7}{2}$时,△PEC与△QFC全等.
如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A-C路径向终点C运动;点Q从B点出发沿B-C-A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.则点P运动时间为1或$\frac{7}{2}$时,△PEC与△QFC全等.
分析 首先根据题意画出图形,然后由三角形全等可知PC=QC,从而得到关于t的方程,然后解得t的值即可.
解答 解:如图1所示;
∵△PEC与△QFC全等,
∴PC=QC.
∴6-t=8-3t.
解得:t=1.
如图2所示:
∵点P与点Q重合,
∴△PEC与△QFC全等,
∴6-t=3t-8.
解得:t=$\frac{7}{2}$.
故答案为:1或$\frac{7}{2}$.
点评 本题主要考查的是全等三角形的性质的应用,根据题意画出图形是解题的关键.漏解是本题的易错点.

练习册系列答案
相关题目
9.已知-1是关于x的一元二次方程x2+nx-5=0的一个根,则另一个根为( )
| A. | -4 | B. | 4 | C. | -5 | D. | 5 |
7. 两个有理数a,b在数轴上位置如图,下列四个式子中运算结果为正数的式子是( )
两个有理数a,b在数轴上位置如图,下列四个式子中运算结果为正数的式子是( )
 两个有理数a,b在数轴上位置如图,下列四个式子中运算结果为正数的式子是( )
两个有理数a,b在数轴上位置如图,下列四个式子中运算结果为正数的式子是( )| A. | $\frac{a}{b}$ | B. | b-a | C. | ab | D. | a+b |
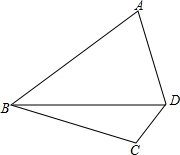 如图,已知四边形ABCD中,AB=24,AD=15,BC=20,CD=7,∠ADB+∠CBD=90°.
如图,已知四边形ABCD中,AB=24,AD=15,BC=20,CD=7,∠ADB+∠CBD=90°.