题目内容
17. 如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C′,则点B转过的路径长为$\frac{\sqrt{3}}{3}$π.
如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C′,则点B转过的路径长为$\frac{\sqrt{3}}{3}$π.
分析 先在△ABC中利用∠ABC的余弦计算出BC=2cos30°=$\sqrt{3}$,再根据旋转的性质得∠BCB′=60°,然后根据弧长公式计算点B转过的路径长.
解答 解:在△ABC中,∵∠ACB=90°,∠ABC=30°,
∴cos∠ABC=$\frac{BC}{AB}$,
∴BC=2cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∵△ABC绕直角顶点C逆时针旋转60°得△A′B′C′,
∴∠BCB′=60°,
∴弧BB′的长=$\frac{60•π•\sqrt{3}}{180}$=$\frac{\sqrt{3}}{3}$π.
故答案为$\frac{\sqrt{3}}{3}$π.
点评 本题考查了转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了弧长的计算.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
6.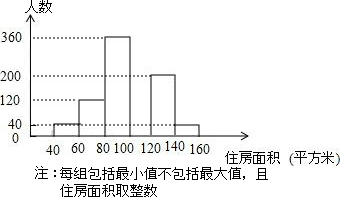 2006年某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部回收.将消费者年收入情况整理后,绘制成如图所示的表格:
2006年某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部回收.将消费者年收入情况整理后,绘制成如图所示的表格:
将消费者打算购买住房的面积的情况整理后,制成部分频数分布直方图,如图所示.
(1)被调查的消费者平均年收入为2.39万元;年收入的中位数是1.8万元;在平均数、中位数这两个数中,中位数更能反映出被调查的消费者年收入的一般水平.
(2)打算购买100~120平方米房子的人数是240人;打算购买住房面积小于100平方米的消费者的人数占被调查人数的百分比为52%.
 2006年某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部回收.将消费者年收入情况整理后,绘制成如图所示的表格:
2006年某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部回收.将消费者年收入情况整理后,绘制成如图所示的表格:| 年收入(万元) | 1.2 | 1.8 | 3 | 5 | 10 |
| 被调查的消费者人数(人) | 200 | 500 | 200 | 70 | 30 |
(1)被调查的消费者平均年收入为2.39万元;年收入的中位数是1.8万元;在平均数、中位数这两个数中,中位数更能反映出被调查的消费者年收入的一般水平.
(2)打算购买100~120平方米房子的人数是240人;打算购买住房面积小于100平方米的消费者的人数占被调查人数的百分比为52%.
 AB是圆O的直径,点C,D都在圆O上,连接CA,CB,DC,DB.已知∠D=30°,BC=3,则AC的长是3$\sqrt{3}$.
AB是圆O的直径,点C,D都在圆O上,连接CA,CB,DC,DB.已知∠D=30°,BC=3,则AC的长是3$\sqrt{3}$.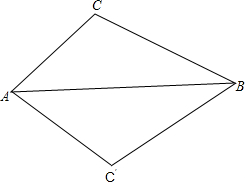 如图所示,把上边的图形沿AB翻折后得到下边的图形,则有三对角对应相等,这三对角分别为∠C=∠C′,∠CAB=∠C′AB,∠CBA=∠C′BA.
如图所示,把上边的图形沿AB翻折后得到下边的图形,则有三对角对应相等,这三对角分别为∠C=∠C′,∠CAB=∠C′AB,∠CBA=∠C′BA.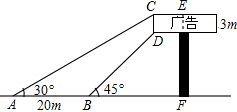 如图,某广告牌竖直矗立在水平地面上,经测量得到如下相关数据:CD=3m,AB=20m,∠CAB=30°,∠DBF=45°,求广告牌的高EF(结果保留根号).
如图,某广告牌竖直矗立在水平地面上,经测量得到如下相关数据:CD=3m,AB=20m,∠CAB=30°,∠DBF=45°,求广告牌的高EF(结果保留根号). 如图所示,DE∥BC,∠1=∠2,求证:EF∥AB.
如图所示,DE∥BC,∠1=∠2,求证:EF∥AB.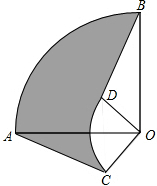 如图,圆心角都是90°的扇形AOB与扇形COD如图叠放在一起,连结AC、BD,若OA=3cm,OC=1cm,则阴影部分的面积为2π平方厘米.
如图,圆心角都是90°的扇形AOB与扇形COD如图叠放在一起,连结AC、BD,若OA=3cm,OC=1cm,则阴影部分的面积为2π平方厘米. 如图,在△ABC中,AB=AC,DE是腰AB上的中垂线,若∠A=30°,求∠EBC的大小.
如图,在△ABC中,AB=AC,DE是腰AB上的中垂线,若∠A=30°,求∠EBC的大小.