题目内容
7.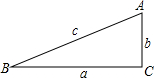 如图,在Rt△ABC中,∠C=90°,根据三角函数定义尝试说明:
如图,在Rt△ABC中,∠C=90°,根据三角函数定义尝试说明:(1)sin2A+cos2A=1;
(2)sinA=cosB;
(3)tanA=$\frac{sinA}{cosA}$.
分析 (1)根据勾股定理,可得a、b、c的关系,根据正弦是对边比斜边,余弦是邻边比斜边,可得答案;
(2)根据勾股定理,可得a、b、c的关系,根据正弦是对边比斜边,余弦是邻边比斜边,可得答案;
(3)根据正弦是对边比斜边,余弦是邻边比斜边,正切是对边比邻边,可得答案.
解答 解:由勾股定理,得
a2+b2=c2.
(1)sin2A+cos2A=$\frac{{a}^{2}}{{c}^{2}}$+$\frac{{b}^{2}}{{c}^{2}}$=$\frac{{c}^{2}}{{c}^{2}}$=1;
(2)sinA=$\frac{a}{c}$,cosB=$\frac{a}{c}$,
sinA=cosB;
(3)tanA=$\frac{a}{b}$,$\frac{sinA}{cosA}$=$\frac{\frac{a}{c}}{\frac{b}{c}}$=$\frac{a}{b}$,
tanA=$\frac{sinA}{cosA}$.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.△ABC≌△DEF,且△ABC的周长为18,若AB=5,AC=6,则EF等于( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
16.如果单项式-$\frac{1}{2}$xay与$\frac{1}{3}$x3yb是同类项,那么a,b的值分别为( )
| A. | 0,3 | B. | 3,0 | C. | 1,3 | D. | 3,1 |
 如图所示,AB是⊙O的直径,CD是⊙O的一条弦,延长DC与BA的延长线相交于点P,且PC=OB,∠BOD=99°,求∠P的度数.
如图所示,AB是⊙O的直径,CD是⊙O的一条弦,延长DC与BA的延长线相交于点P,且PC=OB,∠BOD=99°,求∠P的度数.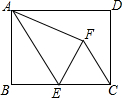 矩形ABCD中,AB=4,BC=6,点E为AB的中点,沿AE将△AEB翻折得到△AFE,sin∠FCE=$\frac{4}{5}$.
矩形ABCD中,AB=4,BC=6,点E为AB的中点,沿AE将△AEB翻折得到△AFE,sin∠FCE=$\frac{4}{5}$.