题目内容
17.已知二次函数y=x2-4x-5.(1)求函数图象的顶点坐标、对称轴及与坐标轴的交点坐标,并画出函数的大致图象;
(2)由图象可知,当x取何值时,-5≤y≤0?
分析 (1)把二次函数化为顶点式求得函数图象的顶点坐标、对称轴,令x=0求出y的值,再令y=0求出x的值与坐标轴的交点坐标,画出函数图象即可;
(2)利用图象直接得出答案即可.
解答 解:(1)∵y=x2-4x-5=(x-2)2-9,
∴顶点坐标为(2,-9),
对称轴为:直线x=2,
∵当x=0时,y=-5,
∴它与y轴的交点坐标为A(0,-5),
当y=0时,x2-4x-5=0,
解得:x=-1或x=5
∴它与x轴的交点坐标为(-1,0)和(5,0);
图象如下:
(2)当-1≤x≤0或4≤x≤5时,-5≤y≤0.
点评 本题考查的是二次函数的性质,熟知二次函数的顶点式及对称轴方程是解答此题的关键.

练习册系列答案
相关题目
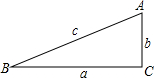 如图,在Rt△ABC中,∠C=90°,根据三角函数定义尝试说明:
如图,在Rt△ABC中,∠C=90°,根据三角函数定义尝试说明: