题目内容
2.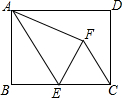 矩形ABCD中,AB=4,BC=6,点E为AB的中点,沿AE将△AEB翻折得到△AFE,sin∠FCE=$\frac{4}{5}$.
矩形ABCD中,AB=4,BC=6,点E为AB的中点,沿AE将△AEB翻折得到△AFE,sin∠FCE=$\frac{4}{5}$.
分析 过E作EH⊥CF于H,由折叠的性质得BE=EF,∠BEA=∠FEA,由点E是BC的中点,得到CE=BE,得到△EFC是等腰三角形,根据等腰三角形的性质得到∠FEH=∠CEH,推出△ABE∽△EHC,求得EH,进一步利用三角函数的意义求得答案即可.
解答 解:如图,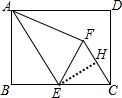
过E作EH⊥CF于H,
由折叠的性质得:BE=EF,∠BEA=∠FEA,
∵点E是BC的中点,
∴CE=BE=3,
∴EF=CE=3,
∴∠FEH=∠CEH,
∴∠AEB+∠CEH=90°,
在矩形ABCD中,
∵∠B=90°,
∴∠BAE+∠BEA=90°,
∴∠BAE=∠CEH,∠B=∠EHC,
∴△ABE∽△EHC,
∴$\frac{AB}{EH}$=$\frac{AE}{CE}$,
∵AE=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴EH=$\frac{12}{5}$,
∴sin∠ECF=$\frac{EH}{CE}$=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了矩形的性质以及勾股定理.

练习册系列答案
相关题目
12.下列各式计算正确的是( )
| A. | 3a+2b=5 | B. | a5÷a=a4 | C. | (-2a2)3=-6a6 | D. | 3a-2=$\frac{1}{9{a}^{2}}$ |
10.二次函数y=2(x+3)2-5的顶点坐标是( )
| A. | (3,-5) | B. | (3,5) | C. | (-3,-5) | D. | (-3,-5) |
14.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,a+c=2b且c-a=$\frac{1}{2}$b,△ABC的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
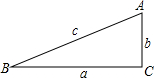 如图,在Rt△ABC中,∠C=90°,根据三角函数定义尝试说明:
如图,在Rt△ABC中,∠C=90°,根据三角函数定义尝试说明: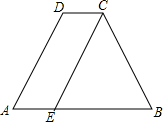 已知:如图,在梯形ABCD中,CD∥AB,AD=BC,E是AB上一点,且AE=CD,∠B=60°,求证:△EBC是等边三角形.
已知:如图,在梯形ABCD中,CD∥AB,AD=BC,E是AB上一点,且AE=CD,∠B=60°,求证:△EBC是等边三角形.