题目内容
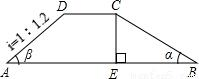 如图,水坝的横截面积是梯形ABCD,迎水坡BC的坡角α为30°,背水坡AD的坡度i,即(tanβ)为1:1.2,坝顶宽DC=2.5m,坝高4.5m.
如图,水坝的横截面积是梯形ABCD,迎水坡BC的坡角α为30°,背水坡AD的坡度i,即(tanβ)为1:1.2,坝顶宽DC=2.5m,坝高4.5m.(1)求:坝底宽AB的长.(结果保留根号)
(2)若把堤坝加高0.5米(整个大坝长5m,不改变坡角与坝底),需要多少土方?
考点:解直角三角形的应用-坡度坡角问题
专题:
分析:(1)作DF⊥AB,可得四边形CDFE为矩形,根据tanβ和α的值即可求得AF,BE的长,即可解题;
(2)根据堤坝底不变坡度不变即可求得增高前和增高后各需要的土方数,即可解题.
(2)根据堤坝底不变坡度不变即可求得增高前和增高后各需要的土方数,即可解题.
解答:解:(1)作DF⊥AB,

∵CE⊥EF,
∴四边形CDFE为矩形,
∴EF=CD,DF=CE,
∵tanβ=1:1.2,
∴AF=1.2DF=5.4m,
∵α=30°,
∴BE=CE•cotα=4.5
m,
∴AB=AF+EF+BE=(7.9+4.5
)m;
(2)堤坝加高0.5米,AB长不变,
堤坝增高前需要土方为
(7.9+4.5
+2.5)×4.5×5方=117+50.625
,
堤坝增高后需要土方为
(7.9+4.5
+2.5)×5×5方=130+56.25
,
故堤坝加高0.5米需要增加土方为(13+5.625
)方.

∵CE⊥EF,
∴四边形CDFE为矩形,
∴EF=CD,DF=CE,
∵tanβ=1:1.2,
∴AF=1.2DF=5.4m,
∵α=30°,
∴BE=CE•cotα=4.5
| 3 |
∴AB=AF+EF+BE=(7.9+4.5
| 3 |
(2)堤坝加高0.5米,AB长不变,
堤坝增高前需要土方为
| 1 |
| 2 |
| 3 |
| 3 |
堤坝增高后需要土方为
| 1 |
| 2 |
| 3 |
| 3 |
故堤坝加高0.5米需要增加土方为(13+5.625
| 3 |
点评:本题考查了坡度坡角的求解,考查了特殊角的三角函数值,考查了三角函数在直角三角形中运用,本题中求得AF,BE的长是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
在平面直角坐标系中,函数y=x2-2x(x≥0)的图象为C1,C1关于原点对称的图象为C2,则直线y=a(a为常数)与C1、C2的交点共有3个,则a的取值范围是( )
| A、a<1 |
| B、-1<a<1 |
| C、-1≤a≤1 |
| D、a>1或a<-1 |
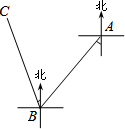 一艘轮船由海平面上A地出发向南偏西60°的方向行驶40海里到达B地,再由B地向北偏西30°的方向行驶30海里到达C地,则A、C两地相距( )
一艘轮船由海平面上A地出发向南偏西60°的方向行驶40海里到达B地,再由B地向北偏西30°的方向行驶30海里到达C地,则A、C两地相距( )| A、30海里 | B、40海里 |
| C、50海里 | D、60海里 |
抛物线y=3x2向下平移3个单位,再向左平移2个单位,得到的抛物线解析式为( )
| A、y=3(x+2)2+3 |
| B、y=3(x-2)2+3 |
| C、y=3(x+2)2-3 |
| D、y=3(x-2)2-3 |
下列说法正确的是( )
| A、有最大的负整数 |
| B、有最小的负整数 |
| C、小数都能化成分数 |
| D、0是最小的整数 |
 在△ABC中,∠C=90°,△ABC的两锐角平分线AD、BE交于点O.
在△ABC中,∠C=90°,△ABC的两锐角平分线AD、BE交于点O.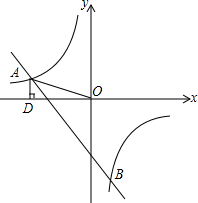 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=