题目内容
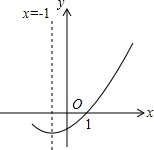
在平面直角坐标系中,函数y=x2-2x(x≥0)的图象为C1,C1关于原点对称的图象为C2,则直线y=a(a为常数)与C1、C2的交点共有3个,则a的取值范围是( )
| A、a<1 |
| B、-1<a<1 |
| C、-1≤a≤1 |
| D、a>1或a<-1 |
考点:二次函数图象与几何变换
专题:
分析:根据关于原点对称的关系,可得C2,根据直线y=a(a为常数)与C1、C2的交点,可得答案.
解答: 解:∵y=x2-2x=(x-1)2-1(x≥0),
解:∵y=x2-2x=(x-1)2-1(x≥0),
∴抛物线C1的顶点坐标为(1,-1).
∵抛物线C1关于原点对称的图象为抛物线C2,
∴抛物线C2的顶点坐标为(1,1).
∴直线y=a(a为常数)与C1、C2的交点共有3个时a的取值范围是-1<a<1.
故选:B.
 解:∵y=x2-2x=(x-1)2-1(x≥0),
解:∵y=x2-2x=(x-1)2-1(x≥0),∴抛物线C1的顶点坐标为(1,-1).
∵抛物线C1关于原点对称的图象为抛物线C2,
∴抛物线C2的顶点坐标为(1,1).
∴直线y=a(a为常数)与C1、C2的交点共有3个时a的取值范围是-1<a<1.
故选:B.
点评:本题考查了二次函数图象与几何变换,根据题意得到图象,由图象解题可以使问题变得直观化,降低题的难度.

练习册系列答案
相关题目
 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0②b=2a;③当-3<x<1时,ax2+bx+c<0;④a-b<m(am+b)(m≠-1).其中正确的命题有( )
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0②b=2a;③当-3<x<1时,ax2+bx+c<0;④a-b<m(am+b)(m≠-1).其中正确的命题有( )| A、1个 | B、2个 | C、3个 | D、4个 |
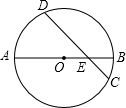 如图,⊙O的直径AB与弦CD交于点,AE=6,BE=2,CD=2
如图,⊙O的直径AB与弦CD交于点,AE=6,BE=2,CD=2| 14 |
| A、30° | B、60° |
| C、45° | D、36° |
已知4个数:(-1)2010,-|-2|,-(-1.5),-32,其中,正数的个数是( )
| A、1 | B、2 | C、3 | D、4 |
 如图,已知y=x2-x-3的图象,请求出方程x2-x-3=0的近似解.
如图,已知y=x2-x-3的图象,请求出方程x2-x-3=0的近似解.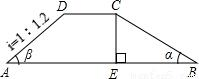 如图,水坝的横截面积是梯形ABCD,迎水坡BC的坡角α为30°,背水坡AD的坡度i,即(tanβ)为1:1.2,坝顶宽DC=2.5m,坝高4.5m.
如图,水坝的横截面积是梯形ABCD,迎水坡BC的坡角α为30°,背水坡AD的坡度i,即(tanβ)为1:1.2,坝顶宽DC=2.5m,坝高4.5m.