题目内容
11.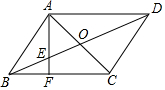 如图,平行四边形ABCD中,AC、BD交于点O,E是OB的中点,AE延长线交BC于F,求证:CF=2BF.
如图,平行四边形ABCD中,AC、BD交于点O,E是OB的中点,AE延长线交BC于F,求证:CF=2BF.
分析 由平行四边形的性质得出OB=D,AD∥BC,证出△BEF∽△DEA,得$\frac{BF}{AD}=\frac{BE}{DE}$=$\frac{1}{3}$,得出BF=$\frac{1}{3}$AD=$\frac{1}{3}$BC,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴OB=D,AD∥BC,
∴△BEF∽△DEA,
∴$\frac{BF}{AD}=\frac{BE}{DE}$,
∵E是OB的中点,
∴DE=3BE,
∴$\frac{BF}{AD}=\frac{BE}{DE}$=$\frac{1}{3}$,
∴BF=$\frac{1}{3}$AD=$\frac{1}{3}$BC,
∴CF=2BF.
点评 本题考查了相似三角形的判定与性质、平行四边形的性质;熟练掌握平行四边形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
相关题目
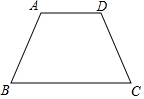 如图,在四边形ABCD中,AD∥BC,AB=CD=6cm,AD=4cm,BC=10cm,求∠D的度数.
如图,在四边形ABCD中,AD∥BC,AB=CD=6cm,AD=4cm,BC=10cm,求∠D的度数.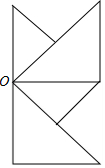 以点O为对称中心,画出与如图所示图形成中心对称的图形.
以点O为对称中心,画出与如图所示图形成中心对称的图形.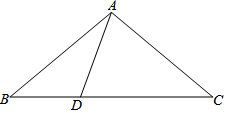 在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.
在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.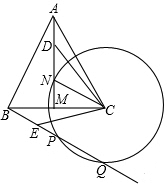 如图,在等边△ABC中,已知AB=8cm,线段AM为BC边上的中线.点N在线段AM上,且MN=3cm,动点D在直线AM上运动,连接CD,△CBE是由△CAD旋转得到的.以点C为圆心,以CN为半径作⊙C与直线BE相交于点P,Q两点.
如图,在等边△ABC中,已知AB=8cm,线段AM为BC边上的中线.点N在线段AM上,且MN=3cm,动点D在直线AM上运动,连接CD,△CBE是由△CAD旋转得到的.以点C为圆心,以CN为半径作⊙C与直线BE相交于点P,Q两点.