题目内容
2.东台成功举办国际自行车公路赛后,许多市民都选择以自行车作为代步工具,如图1所示是一辆自行车的实物图.车架档AC与CD的长分别为45cm,60cm,AC⊥CD,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离.
(结果精确到1cm.参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.7321)
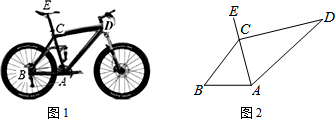
分析 (1)根据AC、CD和AC⊥CD可以求得AD的长;
(2)根据AC、CE和∠EAF的度数可以求得EF的长.
解答 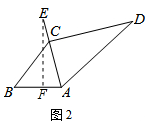 解:(1)∵AC⊥CD,AC=45cm,CD=60cm,
解:(1)∵AC⊥CD,AC=45cm,CD=60cm,
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{4{5}^{2}+6{0}^{2}}=75$cm,
即车架档AD的长是75cm;
(2)作EF⊥AB于点F,如右图所示,
∵AC=45cm,EC=20cm,∠EAB=75°,
∴EF=AE•sin75°=(45+20)×0.9659≈63cm,
即车座点E到车架档AB的距离是63cm.
点评 本题考查解直角三角形的应用,解题的关键是明确题意,利用勾股定理和锐角三角函数进行解答.

练习册系列答案
相关题目
20.下列数据具有一定的排列规律:

若整数2016位于第a行,从左数第b个数,则a+b的值是( )

若整数2016位于第a行,从左数第b个数,则a+b的值是( )
| A. | 63 | B. | 126 | C. | 2015 | D. | 1002 |
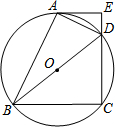 如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.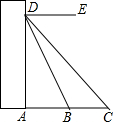 如图,小明家所在住宅楼楼前广场的宽AB为30米,线段BC为AB正前方的一条道路的宽.小明站在家里点D处观察B,C两点的俯角分别为60°和45°,已知DA垂直地面,则这条道路的宽BC为21.96米($\sqrt{3}$≈1.732)
如图,小明家所在住宅楼楼前广场的宽AB为30米,线段BC为AB正前方的一条道路的宽.小明站在家里点D处观察B,C两点的俯角分别为60°和45°,已知DA垂直地面,则这条道路的宽BC为21.96米($\sqrt{3}$≈1.732) 现要建造一段铁路,其路基的横断面ABCD是等腰梯形,上底CD=8米,高DH为2.5米,坡度i=1:1.2.
现要建造一段铁路,其路基的横断面ABCD是等腰梯形,上底CD=8米,高DH为2.5米,坡度i=1:1.2. 据每日邮报报道,按照美国创业家伊隆•马斯克(Elon Musk)最近提出的“超级高铁”(Hyperloop)的设计,超级高铁的速度在理想状态下最高可以达到时速6500公里,预计从北京到纽约仅需2小时,但造价极高,每8公里造价高达620000000美元,数据620000000用科学记数法表示为( )
据每日邮报报道,按照美国创业家伊隆•马斯克(Elon Musk)最近提出的“超级高铁”(Hyperloop)的设计,超级高铁的速度在理想状态下最高可以达到时速6500公里,预计从北京到纽约仅需2小时,但造价极高,每8公里造价高达620000000美元,数据620000000用科学记数法表示为( )