题目内容
14. 现要建造一段铁路,其路基的横断面ABCD是等腰梯形,上底CD=8米,高DH为2.5米,坡度i=1:1.2.
现要建造一段铁路,其路基的横断面ABCD是等腰梯形,上底CD=8米,高DH为2.5米,坡度i=1:1.2.(1)求路基底AB的长;
(2)一段铁路长为2000米,工程由甲、乙两个工程队同时合作完成,原计划需要55天,但在开工时,甲工程队改进了设备,工作效率提高了25%,结果工程提前了5天完成,问这两个工程队原计划每天各完成多少土方?(路基的土方=路基的横断面的面积×路的长度)
分析 (1)要求AB长度需求AE长度和BE长度.依据题意可知,需从C点向AB作垂线,垂足为F,求得BF长度,则可求出答案;
(2)根据计划和实际分别列出两个等量关系式,根据方程组求解.
解答  解:(1)过点C作CF⊥AB于点F,
解:(1)过点C作CF⊥AB于点F,
∵路基的横断面ABCD是等腰梯形,
∴DH=FC,
∵高DH为2.5米,坡度i=1:1.2,
∴$\frac{DH}{AH}$=$\frac{2.5}{AH}$=$\frac{1}{1.2}$,
解得:AH=3,
则AH=BF=3m,
∵DC=8m,
∴HF=8m,
故AB=AH+HF+FB=14m,
答:路基底AB的长为14m;
(2)设原计划甲每天完成x土方,乙每天完成y土方;
v=sh=$\frac{1}{2}$×2.5×(8+14)×2000=55000(立方),
由题意得:$\left\{\begin{array}{l}{55(x+y)=55000}\\{50(1.25x+y)=55000}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=400}\\{y=600}\end{array}\right.$.
答:甲工程队原计划每天完成400土方,乙工程队原计划每天完成600土方.
点评 此题主要考查了解直角三角形的应用以及二元一次方程组的应用,注意过梯形上底的两个顶点向下底引垂线,得到两个直角三角形和一个矩形是常用辅助线方法.

练习册系列答案
相关题目
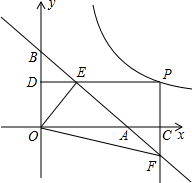 如图,已知直线y=-x+1与x轴交于A点,与y轴交于B点,P(a,b)为双曲线y=$\frac{1}{2x}$(x>0)上一动点,过P点分别作x轴、y轴的垂线,垂足分别为C、D,交直线AB于点E、F
如图,已知直线y=-x+1与x轴交于A点,与y轴交于B点,P(a,b)为双曲线y=$\frac{1}{2x}$(x>0)上一动点,过P点分别作x轴、y轴的垂线,垂足分别为C、D,交直线AB于点E、F 尺规作图:已知△ABC,如图.
尺规作图:已知△ABC,如图.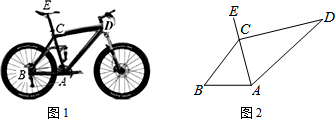
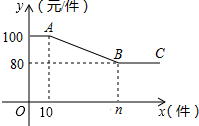 小颖妈妈的网店加盟了“小神龙”童装销售,有一款童装的进价为60元/件,售价为100元/件,因为刚加盟,为了增加销量,准备对大客户制定如下“促销优惠”方案:
小颖妈妈的网店加盟了“小神龙”童装销售,有一款童装的进价为60元/件,售价为100元/件,因为刚加盟,为了增加销量,准备对大客户制定如下“促销优惠”方案: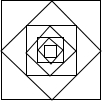 如图,以边长为1的正方形的四边中点为顶点作四边形,再以所得四边形四边中点为顶点作四边形,…依次作下去,图中所作的第n个四边形的周长为$4{(\frac{{\sqrt{2}}}{2})^n}$.
如图,以边长为1的正方形的四边中点为顶点作四边形,再以所得四边形四边中点为顶点作四边形,…依次作下去,图中所作的第n个四边形的周长为$4{(\frac{{\sqrt{2}}}{2})^n}$. 如图,在菱形ABCD中,AB=6,∠A=60°,点E、F分别在AB,BC上,且AE=BF,下列结论中:
如图,在菱形ABCD中,AB=6,∠A=60°,点E、F分别在AB,BC上,且AE=BF,下列结论中: