题目内容
13.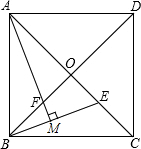 如图,正方形ABCD的边长为2$\sqrt{2}$,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为$\frac{\sqrt{5}}{5}$.
如图,正方形ABCD的边长为2$\sqrt{2}$,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为$\frac{\sqrt{5}}{5}$.
分析 先根据ASA判定△AFO≌△BEO,并根据勾股定理求得BE的长,再判定△BFM∽△BEO,最后根据对应边成比例,列出比例式求解即可.
解答  解:∵正方形ABCD
解:∵正方形ABCD
∴AO=BO,∠AOF=∠BOE=90°
∵AM⊥BE,∠AFO=∠BFM
∴∠FAO=∠EBO
在△AFO和△BEO中
$\left\{\begin{array}{l}{∠AOF=∠BOE}\\{AO=BO}\\{∠FAO=∠EBO}\end{array}\right.$
∴△AFO≌△BEO(ASA)
∴FO=EO
∵正方形ABCD的边长为2$\sqrt{2}$,E是OC的中点
∴FO=EO=1=BF,BO=2
∴直角三角形BOE中,BE=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$
由∠FBM=∠EBO,∠FMB=∠EOB,可得△BFM∽△BEO
∴$\frac{FM}{EO}=\frac{BF}{BE}$,即$\frac{FM}{1}=\frac{1}{\sqrt{5}}$
∴FM=$\frac{\sqrt{5}}{5}$
故答案为:$\frac{\sqrt{5}}{5}$
点评 本题主要考查了正方形,解决问题的关键的掌握全等三角形和相似三角形的判定与性质.解题时注意:正方形的对角线将正方形分成四个全等的等腰直角三角形.

练习册系列答案
相关题目
4. 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
1.若m1,m2,…m2016是从0,1,2这三个数中取值的一列数,且m1+m2+…+m2016=1546,(m1-1)2+(m2-1)2+…+(m2016-1)2=1510,则在m1,m2,…m2016中,取值为2的个数为( )
| A. | 505 | B. | 510 | C. | 520 | D. | 550 |
18.小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:a-b,x-y,x+y,a+b,x2-y2,a2-b2分别对应下列六个字:昌、爱、我、宜、游、美,现将(x2-y2)a2-(x2-y2)b2因式分解,结果呈现的密码信息可能是( )
| A. | 我爱美 | B. | 宜昌游 | C. | 爱我宜昌 | D. | 美我宜昌 |
5. 如图是某工件的三视图,则此工件的表面积为( )
如图是某工件的三视图,则此工件的表面积为( )
 如图是某工件的三视图,则此工件的表面积为( )
如图是某工件的三视图,则此工件的表面积为( )| A. | 15πcm2 | B. | 51πcm2 | C. | 66πcm2 | D. | 24πcm2 |
2.点(2,-4)在反比例函数y=$\frac{k}{x}$的图象上,则下列各点在此函数图象上的是( )
| A. | (2,4) | B. | (-1,-8) | C. | (-2,-4) | D. | (4,-2) |
3.下列图形中,是轴对称图形但不是中心对称图形的是( )
| A. | 正三角形 | B. | 菱形 | C. | 平行四边形 | D. | 正六边形 |
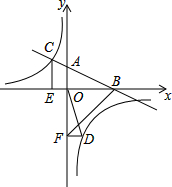 如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=$\frac{m}{x}$的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=$\frac{m}{x}$的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.