题目内容
12.(1)比较下列各式的大小:①|-2|+|3|与|-2+3|;
②|-2|+|-3|与|-2-3|;
③|-2|+|0|与|-2+0|;
(2)请你由(1)归纳总结出|a|+|b|与|a+b|(a、b为有理数)的大小关系,并用文字语言叙述此关系;
(3)根据(2)中的结论,求当|x|+2016=|x-2016|时,x的取值范围.
分析 (1)根据绝对值的定义去绝对值即可求解,
(2)根据(1)中规律即可总结出答案,
(3)根据(2)中结论即可得出答案.
解答 解:(1)∵①|-2|+|3|=5,|-2+3|=1,
∴|-2|+|3|>|-2+3|,
∵②|-2|+|-3|=5,|(-2)+(-3)|=5,
∴|-2|+|-3|=|-2-3|,
∵③|0|+|-2|=2,|-2+0|=2,
∴|-2|+|0|=|-2+0|;
故答案为>,=,=,
(2)根据(1)中规律可得出:|a|+|b|≥|a+b|,
(3)∵|-2016|=2016,
∴|x|+2016=|x|+|-2016|=|x+(-2016)|=|x-2016|,
∴x≤0,
即:当|x|+2016=|x-2016|时,x≤0.
点评 此题考查了有理数的加法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20. 如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )
如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )
 如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )
如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )| A. | 1-$\sqrt{2}$ | B. | $\sqrt{2}$-1 | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-2 |
1.在△ABC中,∠C=90°,tanA=$\frac{12}{5}$,△ABC的周长为60,那么△ABC的面积为( )
| A. | 60 | B. | 30 | C. | 240 | D. | 120 |
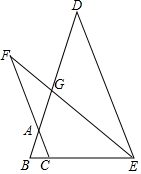 如图,在△ABC中,AB=AC,点D、E、F为三边延长线上的点,且DE∥AC,连接EF交BD于点G,∠BEF+2∠B=180°.
如图,在△ABC中,AB=AC,点D、E、F为三边延长线上的点,且DE∥AC,连接EF交BD于点G,∠BEF+2∠B=180°.