题目内容
7.用适当的方法解下列方程.(1)x2-6x-7=0
(2)x2+2x-5=0.
分析 (1)十字相乘法将左边因式分解,化为两个一元一次方程求解可得;
(2)两边配上一次项系数一半的平方,写成完全平方式后再开方即可得.
解答 解:(1)∵(x+1)(x-7)=0,
∴x+1=0或x-7=0,
解得:x=-1或x=7;
(2)∵x2+2x=5,
∴x2+2x+1=5+1,即(x+1)2=6,
则x+1=±$\sqrt{6}$,
∴x=-1$±\sqrt{6}$.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
相关题目
15.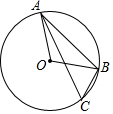 如图,AB是⊙O的弦,C是⊙O上的点,已知∠ABO=40°,则∠ACB的大小为( )
如图,AB是⊙O的弦,C是⊙O上的点,已知∠ABO=40°,则∠ACB的大小为( )
 如图,AB是⊙O的弦,C是⊙O上的点,已知∠ABO=40°,则∠ACB的大小为( )
如图,AB是⊙O的弦,C是⊙O上的点,已知∠ABO=40°,则∠ACB的大小为( )| A. | 40° | B. | 30° | C. | 45° | D. | 50° |
2.已知方程x2-6x+2=0,该方程用配方法变形后的结果为( )
| A. | (x-6)2=34 | B. | (x+6)2=34 | C. | (x-3)2=7 | D. | (x-3)2=11 |
19.若三角形中相等的两边长为5cm,第三边长为6cm,那么第三边上的高为( )
| A. | 6cm | B. | 4cm | C. | 3cm | D. | 2cm |
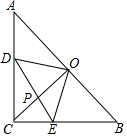 在Rr△ABC中,∠C=90°,AC=BC=1,点O为AB的中点,点D、E分别为AC、AB边上的动点,且保持DO⊥EO,连接CO、DE交于点P.
在Rr△ABC中,∠C=90°,AC=BC=1,点O为AB的中点,点D、E分别为AC、AB边上的动点,且保持DO⊥EO,连接CO、DE交于点P.