题目内容
3.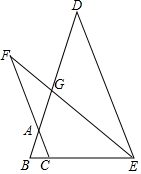 如图,在△ABC中,AB=AC,点D、E、F为三边延长线上的点,且DE∥AC,连接EF交BD于点G,∠BEF+2∠B=180°.
如图,在△ABC中,AB=AC,点D、E、F为三边延长线上的点,且DE∥AC,连接EF交BD于点G,∠BEF+2∠B=180°.(1)当BD=EF时,请找出图中与BE相等的线段,并说明理由.
(2)若BD=kEF,AB=a,cosB=$\frac{1}{6}$,求线段BE的长.(用含有k,a的代数式表示)
分析 (1)由等腰三角形的性质得到∠B=∠ACB,由平行线的性质得到∠DEB=∠ACB,等量代换得到∠DEB=∠B,根据已知条件得到∠EGB=∠B,由等腰三角形的判定得到BE=GE,∵根据全等三角形的性质得到GE=FC,于是得到结论;
(2)作AH⊥BC于H,由cos∠B=$\frac{BH}{AB}=\frac{1}{6}$,得到BH=$\frac{1}{6}$a,根据等腰三角形的性质得到BC=2BH=$\frac{1}{3}$a,根据相似三角形的性质得到BE=GE=3BG,DB=DE=3BE,设CE=x,得到BE=$\frac{1}{3}$a+x,BG=$\frac{1}{9}$a+$\frac{1}{3}$xD得到kx+$\frac{1}{9}$a+$\frac{1}{3}$x=3($\frac{1}{3}$a+x),解方程即可得到结论.
解答  解:(1)当BD=EF时,BE=GE=FC,
解:(1)当BD=EF时,BE=GE=FC,
理由:∵AB=AC,
∴∠B=∠ACB,
∵AC∥DE,
∴∠DEB=∠ACB
∴∠DEB=∠B,
∵∠BEF+2∠B=180°,∠D+2∠B=180°,
∴∠D=∠BEF,
∴∠EGB=180°-∠B-∠BEF,
∴∠EGB=180°-∠B-∠BEF=180°-∠B-∠D=∠BED,
∴∠EGB=∠B,
∴BE=GE,
∵AC∥DE,
∴∠F=∠DEF,
在△CEF与△GDE中,$\left\{\begin{array}{l}{∠F=∠DEF}\\{∠BEF=∠D}\\{EF=DE}\end{array}\right.$,
∴△CEF≌△GDE,
∴GE=FC,
∴BE=GE=CF;
(2)∵∠BAC=∠D=∠BEG,∠B=∠B=∠B,
∴△ABC∽△EBG∽△DBE,
作AH⊥BC于H,
∵cos∠B=$\frac{BH}{AB}=\frac{1}{6}$,
∴BH=$\frac{1}{6}$a,
∵AB=AC,AH⊥BC,
∴BC=2BH=$\frac{1}{3}$a,
∵△ABC∽△EBG∽△DBE,
∴BE=GE=3BG,DB=DE=3BE,
设CE=x,
∴BE=$\frac{1}{3}$a+x,
∴BG=$\frac{1}{9}$a+$\frac{1}{3}$x,
∵∠F=∠DEF,∠BEF=∠D,
∴△CEF∽△GDE,
∴$\frac{DE}{EF}=\frac{DG}{CE}$=k,
∴DG=kCE=kx,
∴BD=DG+BG=3BE,
即kx+$\frac{1}{9}$a+$\frac{1}{3}$x=3($\frac{1}{3}$a+x),
∴x=$\frac{8a}{3k-24}$,
∴BE=$\frac{1}{3}$a+$\frac{8a}{3k-24}$=$\frac{ka}{3k-24}$.
点评 本题考查了全等三角形的判断和性质,等腰三角形的性质,平行线的性质,相似三角形的判定和性质,熟练正确全等三角形的判断和性质是解题的关键.

 如图所示的几何体三视图的主视图是( )
如图所示的几何体三视图的主视图是( )| A. |  | B. |  | C. |  | D. |  |
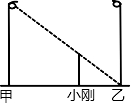 如图,甲、乙两盏路灯相距30米,一天晚上,当小刚从路灯甲底部向路灯乙底部直行25米时,发现自己的身影顶部正好接触到路灯乙的底部,已知小刚的身高为1.5米,那么路灯甲的高为( )
如图,甲、乙两盏路灯相距30米,一天晚上,当小刚从路灯甲底部向路灯乙底部直行25米时,发现自己的身影顶部正好接触到路灯乙的底部,已知小刚的身高为1.5米,那么路灯甲的高为( )| A. | 9米 | B. | 8米 | C. | 7米 | D. | 6米 |
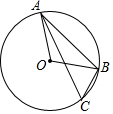 如图,AB是⊙O的弦,C是⊙O上的点,已知∠ABO=40°,则∠ACB的大小为( )
如图,AB是⊙O的弦,C是⊙O上的点,已知∠ABO=40°,则∠ACB的大小为( )| A. | 40° | B. | 30° | C. | 45° | D. | 50° |
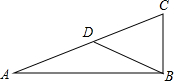 如图,已知在△ABC中,AB=12,BC=5,AC=13,D为AC的中点,连接BD,求BD的长度.
如图,已知在△ABC中,AB=12,BC=5,AC=13,D为AC的中点,连接BD,求BD的长度.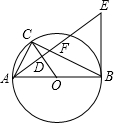 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,经过点A作AE⊥OC,垂足为点D,AE与BC交于点F,与过点B的直线交于点E,且EB=EF.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,经过点A作AE⊥OC,垂足为点D,AE与BC交于点F,与过点B的直线交于点E,且EB=EF.