题目内容
1.数学活动:将形状不同的三张矩形纸片按照如图的方式折叠,BE、DF分别是折痕.折叠后点A、C分别落在矩形对角线BD上的点P、点Q处.(1)如图1,折叠后的四边形BEDF是什么四边形?请说明理由.
(2)如图2,折叠后若点P与点Q重合,则矩形ABCD中$\frac{BC}{AB}$的值是$\sqrt{3}$(直接写答案).
(3)如图3,延长 EP交BC边于点G,延长 FQ交AD边于点H,若四边形EGFH是菱形,AD=10,求矩形的宽AB的长.

分析 (1)直接利用翻折变换的性质得出,∠EBD=∠ABE=$\frac{1}{2}$∠ABD,∠FDB=∠CDF=$\frac{1}{2}$∠CDB,进而得出EB∥DF,又DE∥BF,即可得出答案;
(2)利用CD=$\frac{1}{2}$BD,又∠C=90°,得出∠DBC=30°,即可得出$\frac{BC}{AB}$的值;
(3)利用翻折变换的性质得出BD=BP+PQ+QD=AB+AB+AB,进而利用勾股定理得出AB的长.
解答 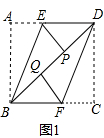 解:(1)如图1,
解:(1)如图1,
∵AB∥CD,
∴∠ABD=∠CDB,
由折叠的性质可知,∠EBD=∠ABE=$\frac{1}{2}$∠ABD,∠FDB=∠CDF=$\frac{1}{2}$∠CDB,
∴∠EBD=∠FDB,
∴EB∥DF,又DE∥BF,
∴折叠后的四边形BEDF是平行四边形;
(2)如图2,∵DC=DP,BA=BP,DC=BA,
∴CD=$\frac{1}{2}$BD,又∠C=90°,
∴∠DBC=30°,
∴$\frac{BC}{AB}$=$\sqrt{3}$,
故答案为:$\sqrt{3}$;
(3)如图3,∵AB=PB,CD=QD,EP⊥BD,FQ⊥DQ,
∴PQ是菱形EGFH的高,即EH与GF间的距离为PQ,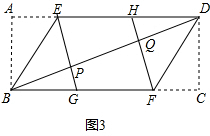
故PQ=AB=CD,
∴BD=BP+PQ+QD=AB+AB+AB,
∴3AB=BD,
∴设AB=x,则BD=3x,
∵AD=10,
∴x2+102=(3x)2,
解得:x=±$\frac{5\sqrt{2}}{2}$(负数舍去),
即矩形的宽AB的长为:$\frac{5\sqrt{2}}{2}$.
点评 此题主要考查了四边形综合以及勾股定理和翻折变换的性质、平行四边形的判定等知识,正确表示出BD与AB的关系是解题关键.

练习册系列答案
相关题目
10.沪蓉高速大别山特长隧道贯通,全长4901m,将4901用科学记数法表示为( )
| A. | 49.01×102 | B. | 4.901×103 | C. | 490.1×10 | D. | 0.4901×104 |
10.世上最小开花植物的果实质量只有0.00000007克,用科学记数法表示是( )
| A. | 7.0×108 | B. | 0.7×109 | C. | 7.0×10-8 | D. | 0.7×10-9 |
11.观察表格再回答下列问题.
问:
(1)被开方数a的小数点位置移动和它的算术平方根$\sqrt{a}$的小数点位置移动有无规律?若有规律,请写出它的移动规律.
(2)利用你在(1)中发现的规律,已知:$\sqrt{3}$≈1.732,求出$\sqrt{0.03}$的值;
(3)已知$\sqrt{a}$=1800,-$\sqrt{3.24}$=-1.8,你能求出a的值吗?
(4)试比较$\sqrt{a}$与a的大小.
| a | … | 0.000001 | 0.0001 | 0.01 | 1 |
| $\sqrt{a}$ | … | 0.001 | 0.01 | 0.1 | 1 |
| a | 100 | 10000 | 1000000 | … | |
| $\sqrt{a}$ | 10 | 100 | 1000 | … |
(1)被开方数a的小数点位置移动和它的算术平方根$\sqrt{a}$的小数点位置移动有无规律?若有规律,请写出它的移动规律.
(2)利用你在(1)中发现的规律,已知:$\sqrt{3}$≈1.732,求出$\sqrt{0.03}$的值;
(3)已知$\sqrt{a}$=1800,-$\sqrt{3.24}$=-1.8,你能求出a的值吗?
(4)试比较$\sqrt{a}$与a的大小.
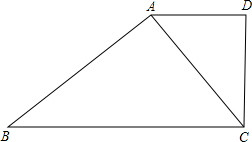 已知:如图,在四边形ABCD中,∠BAC=∠ADC=90°,AD=a,BC=b,$\sqrt{AC}$=$\sqrt{ab}$.求证:DC⊥BC.
已知:如图,在四边形ABCD中,∠BAC=∠ADC=90°,AD=a,BC=b,$\sqrt{AC}$=$\sqrt{ab}$.求证:DC⊥BC.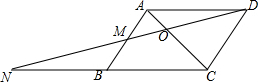 已知:在平行四边形ABCD中,AD:DC=2:3,O是对角线AC上的一点,连接DO并延长,与AB交于点M,与CB的延长线交于点N.若AD=4,NC=10,∠ABC=60°,则OM的长为$\frac{8}{5}$.
已知:在平行四边形ABCD中,AD:DC=2:3,O是对角线AC上的一点,连接DO并延长,与AB交于点M,与CB的延长线交于点N.若AD=4,NC=10,∠ABC=60°,则OM的长为$\frac{8}{5}$.