题目内容
6.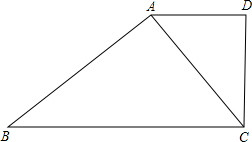 已知:如图,在四边形ABCD中,∠BAC=∠ADC=90°,AD=a,BC=b,$\sqrt{AC}$=$\sqrt{ab}$.求证:DC⊥BC.
已知:如图,在四边形ABCD中,∠BAC=∠ADC=90°,AD=a,BC=b,$\sqrt{AC}$=$\sqrt{ab}$.求证:DC⊥BC.
分析 根据勾股定理分别求出AD、CD、AB,再求出△ADC和△CBA的三边之比,进而证得△ADC∽△CBA,得到∠ACD=∠ACB,推出AD‖BC,从而推出结论.
解答 证明:在Rt△ABC中,
∵AD=a,$\sqrt{AC}$=$\sqrt{ab}$,
∴CD=$\sqrt{ab{-a}^{2}}$,
在Rt△ABC中,
∵BC=b,$\sqrt{AC}$=$\sqrt{ab}$,
∴AB=$\sqrt{{b}^{2}-ab}$,
∵$\frac{AC}{BC}=\frac{\sqrt{ab}}{b}$,$\frac{AD}{AC}=\frac{a}{\sqrt{ab}}$=$\frac{\sqrt{ab}}{b}$,
$\frac{CD}{AB}=\frac{\sqrt{(ab-{a}^{2})}}{\sqrt{{b}^{2}-ab}}$=$\frac{\sqrt{ab}}{b}$,
∴△ADC∽△CBA,
∴∠ACD=∠ACB,
∴AD‖BC,
∴∠BCD+∠ADC=90°,
∵∠ADC=90°,
∴∠BCD=90°,
∴DC⊥BC.
点评 本题考查了相似三角形的判定和性质,勾股定理,平行线的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
8.“a与b的$\frac{1}{10}$的差”,用代数式表示为( )
| A. | $\frac{1}{10}$(a-b) | B. | a-$\frac{1}{10}$b | C. | a+b-$\frac{1}{10}$ | D. | a-b-$\frac{1}{10}$ |
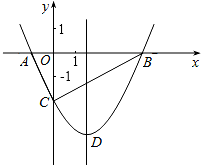 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).
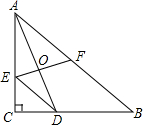 在△ABC中,∠C=90°,AC=BC,点D在BC上,DE∥AB交AC于E,点F为AB中点,连接EF.若EF⊥AD,AO=3,则OD=2.
在△ABC中,∠C=90°,AC=BC,点D在BC上,DE∥AB交AC于E,点F为AB中点,连接EF.若EF⊥AD,AO=3,则OD=2.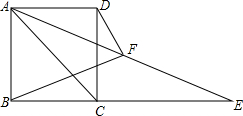 如图,矩形ABCD,过点A作∠DAC的角平分线与BC的延长线相交于点E.
如图,矩形ABCD,过点A作∠DAC的角平分线与BC的延长线相交于点E.