题目内容
13.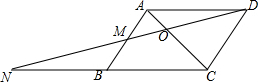 已知:在平行四边形ABCD中,AD:DC=2:3,O是对角线AC上的一点,连接DO并延长,与AB交于点M,与CB的延长线交于点N.若AD=4,NC=10,∠ABC=60°,则OM的长为$\frac{8}{5}$.
已知:在平行四边形ABCD中,AD:DC=2:3,O是对角线AC上的一点,连接DO并延长,与AB交于点M,与CB的延长线交于点N.若AD=4,NC=10,∠ABC=60°,则OM的长为$\frac{8}{5}$.
分析 根据四边形ABCD是平行四边形,得到AD=BC=4,AB=CD=6,通过△BNM∽△CND,得到$\frac{BM}{CD}=\frac{BN}{CN}$,求出BM=$\frac{18}{5}$,AM=$\frac{12}{5}$,根据平行线分线段成比例得到OM=$\frac{2}{7}$DM=$\frac{4}{35}$DN,过D作DH⊥BC于H,解直角三角形即可得到结论.
解答 解:∵AD:DC=2:3,AD=4,
∴CD=6,
∵四边形ABCD是平行四边形,
∴AD=BC=4,AB=CD=6,
∵CN=10,
∴BN=6,
∵AB∥CD,
∴△BNM∽△CND,
∴$\frac{BM}{CD}=\frac{BN}{CN}$,
∴BM=$\frac{18}{5}$,AM=$\frac{12}{5}$,
∵BM∥CD,
∴NM:MD=BN:BC=6:4=3:2,
∴DM:DN=2:5,
∴OM:OD=AM:CD=$\frac{12}{5}$:6=2:5,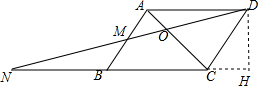
∴OM=$\frac{2}{7}$DM=$\frac{4}{35}$DN,
过D作DH⊥BC交BC的延长线于H,
∵∠ABC=60°,
∴∠DCH=60°,
∴CH=$\frac{1}{2}$CD=3,DH=3$\sqrt{3}$,
∴DN=$\sqrt{D{H}^{2}+H{N}^{2}}$=14,
∴OM=14×$\frac{4}{35}$=$\frac{8}{5}$.
故答案为:$\frac{8}{5}$.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质,勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
17.下列说法正确的是( )
| A. | 任何数都有两个平方根 | B. | 若a2=b2,则a=b | ||
| C. | $\sqrt{4}$=±2 | D. | -8的立方根是-2 |
2.最薄的金箔的厚度为0.000000091m,将0.000000091用科学记数法表示为( )
| A. | 9.1×108 | B. | 9.1×109 | C. | 9.1×10-8 | D. | 9.1×10-9 |

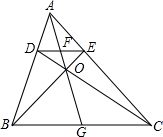 如图所示,已知在△ABC中,作平行于BC的直线交AB于D,交AC于E,如果BE和CD相交于O,AO和DE相交于F,AO的延长线和BC交于G,证明:
如图所示,已知在△ABC中,作平行于BC的直线交AB于D,交AC于E,如果BE和CD相交于O,AO和DE相交于F,AO的延长线和BC交于G,证明: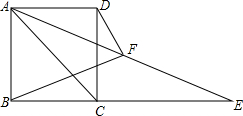 如图,矩形ABCD,过点A作∠DAC的角平分线与BC的延长线相交于点E.
如图,矩形ABCD,过点A作∠DAC的角平分线与BC的延长线相交于点E.