题目内容
7.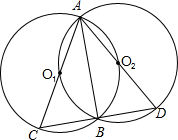 如图,两等圆⊙O1和⊙O2相交于A、B两点,且两圆相互过圆心,过点B作任一直线,分别交⊙O1、⊙O2于C、D两点,接AC、AD.试猜想△ACD的形状,并说明理由.
如图,两等圆⊙O1和⊙O2相交于A、B两点,且两圆相互过圆心,过点B作任一直线,分别交⊙O1、⊙O2于C、D两点,接AC、AD.试猜想△ACD的形状,并说明理由.
分析 首先证明△AO1O2,△BO1O2都是等边三角形,得到∠AO1B=∠AO2B=120°,再根据∠ACD=$\frac{1}{2}$∠AO1B,∠ADC=$\frac{1}{2}$∠AO2B,即可解决问题.
解答 解:如图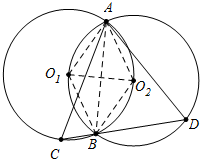 连接AB,AO1,O1B,O1O2,AO2,BO2.
连接AB,AO1,O1B,O1O2,AO2,BO2.
∵AO1=O1B=O1O2=AO2=BO2,
∴△AO1O2,△BO1O2是都等边三角形,
∴∠AO1O2=∠BO1O2=∠AO2O1=∠BO2O1=60°,
∴∠AO1B=∠AO2B=120°,
∴∠ACD=$\frac{1}{2}$∠AO1B=60°,∠ADC=$\frac{1}{2}$∠AO2B=60°,
∴∠ACD=∠ADC=∠CAD=60°,
∴△ACD是等边三角形.
点评 本题考查圆与位置关系,同弧所对的圆周角与圆心角的关系、等边三角形的判定等知识,解题的关键是发现△AO1O2,△BO1O2都是等边三角形,属于中考常考题型.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
7.不等式组$\left\{\begin{array}{l}x+2>0\\ 2x-1≤0\end{array}\right.$的所有整数解是( )
| A. | -1、0 | B. | -2、-1 | C. | 0、1 | D. | -2、-1、0 |
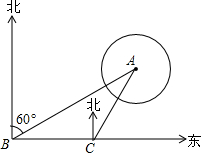 如图,某公园有一小亭A,它周围100米内是文物保持区,某勘探队员在公园由西向东行走,在B处测得小亭A在北偏东60°的方向上,行走200米后到达C处,此时测得小亭A在北偏东30°的方向上,若该公园打算沿BC的方向修一条笔直的小路,则此小路是否会通过文物保护区?请通过计算说明.
如图,某公园有一小亭A,它周围100米内是文物保持区,某勘探队员在公园由西向东行走,在B处测得小亭A在北偏东60°的方向上,行走200米后到达C处,此时测得小亭A在北偏东30°的方向上,若该公园打算沿BC的方向修一条笔直的小路,则此小路是否会通过文物保护区?请通过计算说明. 如图所示,已知⊙O1与⊙O2相交于A、B两点,直线O1O2交⊙O1于P点,直线PA交⊙O2于C点,直线PB交⊙O2于D点.求证:O1O2⊥CD.
如图所示,已知⊙O1与⊙O2相交于A、B两点,直线O1O2交⊙O1于P点,直线PA交⊙O2于C点,直线PB交⊙O2于D点.求证:O1O2⊥CD.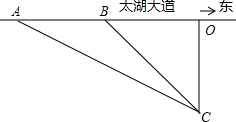 某同学为了检测车速,设计如下方案如图,观测点C选在东西方向的太湖大道上O点正南方向120米处.这时,一辆小轿车沿太湖大道由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为3秒,且∠ACO=60°,∠BCO=45°
某同学为了检测车速,设计如下方案如图,观测点C选在东西方向的太湖大道上O点正南方向120米处.这时,一辆小轿车沿太湖大道由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为3秒,且∠ACO=60°,∠BCO=45° 如图∠1=75°,∠A=60°,∠B=45°
如图∠1=75°,∠A=60°,∠B=45°