题目内容
12.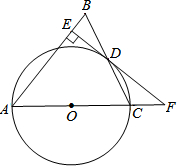 如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.(1)求证:EF是⊙O的切线;
(2)若EB=$\frac{3}{2}$,且sin∠CFD=$\frac{3}{5}$,求⊙O的半径与线段AE的长.
分析 (1)连结OD,如图,由AB=AC得到∠B=∠ACD,由OC=OD得到∠ODC=∠OCD,则∠B=∠ODC,于是可判断OD∥AB,然后利用DE⊥AB得到OD⊥EF,然后根据切线的判定定理得到结论;
(2)在Rt△ODF利用正弦的定义得到sin∠OFD=$\frac{OD}{OF}$=$\frac{3}{5}$,则可设OD=3x,OF=5x,所以AB=AC=6x,AF=8x,在Rt△AEF中由于sin∠AFE=$\frac{AE}{AF}$=$\frac{3}{5}$,可得到AE=$\frac{24}{5}$x,接着表示出BE得到$\frac{6}{5}$x=$\frac{3}{2}$,解得x=$\frac{5}{4}$,于是可得到AE和OD的长.
解答 (1)证明:连结OD,如图,
∵AB=AC,
∴∠B=∠ACD,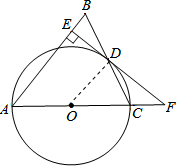
∵OC=OD,
∴∠ODC=∠OCD,
∴∠B=∠ODC,
∴OD∥AB,
∵DE⊥AB,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)解:在Rt△ODF,sin∠OFD=$\frac{OD}{OF}$=$\frac{3}{5}$,
设OD=3x,则OF=5x,
∴AB=AC=6x,AF=8x,
在Rt△AEF中,∵sin∠AFE=$\frac{AE}{AF}$=$\frac{3}{5}$,
∴AE=$\frac{3}{5}$•8x=$\frac{24}{5}$x,
∵BE=AB-AE=6x-$\frac{24}{5}$x=$\frac{6}{5}$x,
∴$\frac{6}{5}$x=$\frac{3}{2}$,解得x=$\frac{5}{4}$,
∴AE=$\frac{24}{5}$•$\frac{5}{4}$=6,
OD=3•$\frac{5}{4}$=$\frac{15}{4}$,
即⊙O的半径长为$\frac{15}{4}$.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.灵活应用三角函数的定义是解决(2)小题的关键.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案| A. | 2x | B. | 2x2 | C. | -2x | D. | -2 |
| A. | -1、0 | B. | -2、-1 | C. | 0、1 | D. | -2、-1、0 |
| A. | x(2x-1)=2x2-1 | B. | $\frac{x+3}{{x}^{2}-9}$=$\frac{1}{x-3}$ | C. | (a+2)2=a2+4 | D. | (x+2)(x-3)=x2+x-6 |
| A. | x2-3x+1=x2-x•3+32-32+1 | B. | 2x2-3x+1=x2-2•x$•\frac{3}{2}$+($\frac{3}{2}$)2-($\frac{3}{2}$)2+1 | ||
| C. | x2-3x+1=x2-2•x$•\frac{3}{2}$+($\frac{3}{2}$)2+1 | D. | 2x2-3x+1=2[x2-2$•x•\frac{3}{4}$+($\frac{3}{4}$)2-($\frac{3}{4}$)2+$\frac{1}{2}$] |
 如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为$\frac{1}{4}$πcm2.
如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为$\frac{1}{4}$πcm2.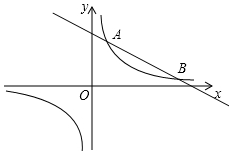 如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1). 如图所示,已知⊙O1与⊙O2相交于A、B两点,直线O1O2交⊙O1于P点,直线PA交⊙O2于C点,直线PB交⊙O2于D点.求证:O1O2⊥CD.
如图所示,已知⊙O1与⊙O2相交于A、B两点,直线O1O2交⊙O1于P点,直线PA交⊙O2于C点,直线PB交⊙O2于D点.求证:O1O2⊥CD.