题目内容
14．
如图，已知直线a、b被直线c所截．若a∥b，∠1=120°，则∠2的度数为（ ）| A． | 50° | B． | 60° | C． | 120° | D． | 130° |
分析 根据邻补角的定义求出∠3，再根据两直线平行，同位角相等解答．
解答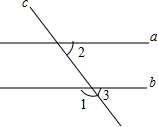 
解：如图，∠3=180°-∠1=180°-120°=60°，
∵a∥b，
∴∠2=∠3=60°．
故选：B．
点评 本题考查了平行线的性质，邻补角的定义，是基础题，熟记性质是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
4．已知a=（-$\frac{1}{2.78}$）67，b=（-$\frac{1}{2.78}$）68，c=（-$\frac{1}{2.78}$）69，判断a、b、c三数的大小关系为下列何者？（ ）
| A． | a＞b＞c | B． | b＞a＞c | C． | b＞c＞a | D． | c＞b＞a |
5．某次列车平均提速20km/h，用相同的时间，列车提速前行驶400km，提速后比提速前多行驶100km，设提速前列车的平均速度为xkm/h，下列方程正确的是（ ）
| A． | $\frac{400}{x}$=$\frac{400+100}{x+20}$ | B． | $\frac{400}{x}$=$\frac{400-100}{x-20}$ | ||
| C． | $\frac{400}{x}$=$\frac{400+100}{x-20}$ | D． | $\frac{400}{x}$=$\frac{400-100}{x+20}$ |
如图，C为半圆内一点，O为圆心，直径AB长为2cm，∠BOC=60°，∠BCO=90°，将△BOC绕圆心O逆时针旋转至△B′OC′，点C′在OA上，则边BC扫过区域（图中阴影部分）的面积为$\frac{1}{4}$πcm2．
19．某体校要从四名射击选手中选拔一名参加省体育运动会，选拔赛中每名选手连续射靶10次，他们各自的平均成绩$\overline{x}$及其方差S2如表所示：
如果要选出一名成绩高且发挥稳定的选手参赛，则应选择的选手是（ ）
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$（环） | 8.4 | 8.6 | 8.6 | 7.6 |
| S2 | 0.74 | 0.56 | 0.94 | 1.92 |
| A． | 甲 | B． | 乙 | C． | 丙 | D． | 丁 |
如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（-3，5），B（-2，1），C（-1，3）．
3．计算：5x-3x=（ ）
| A． | 2x | B． | 2x2 | C． | -2x | D． | -2 |
如图所示，已知⊙O1与⊙O2相交于A、B两点，直线O1O2交⊙O1于P点，直线PA交⊙O2于C点，直线PB交⊙O2于D点．求证：O1O2⊥CD．