题目内容
1.用适当的方法解下列一元二次方程.(1)(x-1)2+2x(x-1)=0;
(2)3y2+1=2$\sqrt{3}$y.
分析 (1)左边提取公因式分解后即可得;
(2)整理成一般式后,根据完全平方公式分解因式即可得.
解答 解:(1)(x-1)(x-1+2x)=0,
即(x-1)(3x-1)=0,
∴x-1=0或3x-1=0,
解得:x=1或x=$\frac{1}{3}$;
(2)整理,得:3y2-2$\sqrt{3}$y+1=0,
即($\sqrt{3}$y-1)2=0,
∴$\sqrt{3}$y-1=0,
解得:y=$\frac{\sqrt{3}}{3}$.
点评 本题主要考查因式分解法解一元二次方程的能力,熟练掌握因式分解的基本方法是解题的关键.

练习册系列答案
相关题目
9.某电器超市销售每台进价分别200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元,不少于5340元的金额再采购这两种型号的电风扇共30台,求A、B两种型号的电风扇的采购方案;
(3)在(2)的条件下,超市销售完这30台电风扇,用所获利润再次购进A/B两种型号的电风扇且恰好全部售出,请直接写出再次销售的A、B两种型号的电风扇各多少台所获最大利润?最大利润是多少?
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第一周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元,不少于5340元的金额再采购这两种型号的电风扇共30台,求A、B两种型号的电风扇的采购方案;
(3)在(2)的条件下,超市销售完这30台电风扇,用所获利润再次购进A/B两种型号的电风扇且恰好全部售出,请直接写出再次销售的A、B两种型号的电风扇各多少台所获最大利润?最大利润是多少?
6.如图,某数学小组在课外实践活动中,用电钻将四个质地均匀、质量相等的木质小正方体,分别从不同方向钻一个直径一样的直圆孔,再用天平分别称得下列小正方体的质量,下列说法中正确的是( )
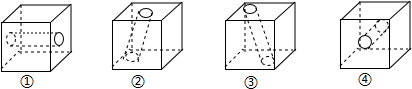

| A. | ①和④更重 | B. | ③最轻 | C. | 质量仍然一样 | D. | ②和③更重 |
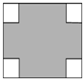 如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化. 如图,将△ABC纸片沿DE折叠,使点A落在四边形BCDE内点A′的位置,已知∠A=30°,∠1=20°,求∠2的度数.
如图,将△ABC纸片沿DE折叠,使点A落在四边形BCDE内点A′的位置,已知∠A=30°,∠1=20°,求∠2的度数. 如图所示,各边都相等的五边形ABCDE中,∠ABC=2∠DBE,求∠ABC.
如图所示,各边都相等的五边形ABCDE中,∠ABC=2∠DBE,求∠ABC. 如图所示,矩形OABC的顶点A,C分别在x,y轴的正半轴上,点D为对角线OB的中点,点E(6,n)在边AB上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D,E,且tan∠BOA=$\frac{1}{3}$.
如图所示,矩形OABC的顶点A,C分别在x,y轴的正半轴上,点D为对角线OB的中点,点E(6,n)在边AB上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D,E,且tan∠BOA=$\frac{1}{3}$.