题目内容
16. 如图,在折纸活动中,李红制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿DE折叠压平,A与F重合,若∠A=70°,则∠1+∠2等于( )
如图,在折纸活动中,李红制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿DE折叠压平,A与F重合,若∠A=70°,则∠1+∠2等于( )| A. | 70° | B. | 110° | C. | 130° | D. | 140° |
分析 先根据图形翻折变化的性质得出△ADE≌△FDE,∠AED=∠FED,∠ADE=∠FDE,再根据三角形内角和定理求出∠AED+∠ADE及∠FED+∠FDE的度数,然后根据平角的性质即可求出答案.
解答 解:∵△FDE是△ABC翻折变换而成,
∴∠AED=∠FED,∠ADE=∠FDE,∠A=∠F=70°,
∴∠AED+∠ADE=∠FED+∠FDE=180°-70°=110°,
∴∠1+∠2=360°-2×110°=140°.
故选D.
点评 本题考查的是三角形内角和定理及翻折变换,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
7.下列不等式变形正确的是( )
| A. | 若a>b,则a-2>b-2 | B. | 若$-\frac{1}{2}a<2$,则a<-4 | ||
| C. | 若a>b,则1-2a>1-2b | D. | 若a<b,则ac2<bc2 |
8. 如图所示几何体的主视图是( )
如图所示几何体的主视图是( )
 如图所示几何体的主视图是( )
如图所示几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |

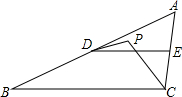 如图,在△ABC中,∠A=50°,DE∥BC,若PC平分∠ACB,DP平分∠ADE,则∠DPC=115°.
如图,在△ABC中,∠A=50°,DE∥BC,若PC平分∠ACB,DP平分∠ADE,则∠DPC=115°. 利用一面长为22米的墙和46米的篱笆围成如图所示的矩形菜地,菜地有2个2米宽的门,门用其它材料.
利用一面长为22米的墙和46米的篱笆围成如图所示的矩形菜地,菜地有2个2米宽的门,门用其它材料.