题目内容
6.如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系,并请你从四个图形中任选一个说明你所探究的结论的正确性.
分析 在前两个图中,可过点P作AB的平行线,根据平行线的性质可得到结论;在后两个图中可根据平行线的性质和三角形外角的性质得到结论.
解答 解:
在第一个图中有∠APC+∠PAB+PCD=360°,
在第二个图中有∠APC=∠PAB+∠PCD,
在第三个图中有∠APC=∠PCD-∠PAB,
在第四个图中有∠APC=∠PAB-∠PCD.
以图(1)为例说明理由:
如图,过点P做PM∥AB,
∵AB∥CD,
∴PM∥CD,
∴∠APM+∠A=180°,∠CPM+∠C=180°,
两式相加得∠A+∠C+∠APM+∠CPM=360°,
即∠APC+∠PAB+∠PCD=360°.
点评 本题主要考查平行线的性质,掌握平行线的性质是解题的关键,即①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
16.甲、乙两人加工同一种玩具,甲加工90个玩具与乙加工120玩具所用的天数相同,已知甲、乙两人每天共加工35个玩具.若设甲每天加工x个玩具,则根据题意列方程( )
| A. | $\frac{120}{x}$=$\frac{90}{35-x}$ | B. | $\frac{90}{x}$=$\frac{120}{35+x}$ | C. | $\frac{90}{3x}$=$\frac{120}{35}$ | D. | $\frac{90}{x}$=$\frac{120}{35-x}$ |
17.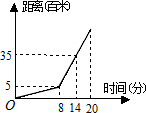 某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )
某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )
 某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )
某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )| A. | 仍会迟到2分钟到校 | B. | 刚好按时到校 | ||
| C. | 可以提前2分钟到校 | D. | 可以提前5分钟到校 |
18.己知反比例函数$y=\frac{m-2}{x}$(m为常数),当x>0时,y随x的增大而增大,则m的取值范围是( )
| A. | m>0 | B. | m>2 | C. | m<0 | D. | m<2 |
16. 如图,在折纸活动中,李红制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿DE折叠压平,A与F重合,若∠A=70°,则∠1+∠2等于( )
如图,在折纸活动中,李红制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿DE折叠压平,A与F重合,若∠A=70°,则∠1+∠2等于( )
 如图,在折纸活动中,李红制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿DE折叠压平,A与F重合,若∠A=70°,则∠1+∠2等于( )
如图,在折纸活动中,李红制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿DE折叠压平,A与F重合,若∠A=70°,则∠1+∠2等于( )| A. | 70° | B. | 110° | C. | 130° | D. | 140° |