题目内容
9.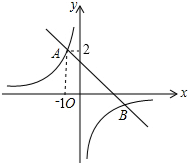 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,2),则另一个交点B的坐标为( )
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,2),则另一个交点B的坐标为( )| A. | (-2,1) | B. | (2,1) | C. | (1,-2) | D. | (2,-1) |
分析 根据反比例函数和一次函数图象上点的坐标特征,将A点坐标代入求得k、b的值,再联立两函数方程求得另一交点坐标.
解答 解:将A点坐标代入y=-x+b和y=$\frac{k}{x}$可求得k=-2,b=1,
所以,直线为y=-x+1,反比例函数为y=-$\frac{2}{x}$,
解$\left\{\begin{array}{l}{y=-x+1}\\{y=-\frac{2}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$,
所以另一点(2,-1);
故另一个交点B的坐标为(2,-1).
故选D.
点评 本题考查了反比例函数和一次函数的解得问题,解答本题的关键是要理解两函数交点和方程组的解的对应关系.同时同学们要掌握解方程组的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.如果a是b的一个平方根,则b的算术平方根是( )
| A. | a | B. | -a | C. | ±a | D. | |a| |
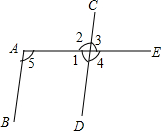 如图,写出所有能使AB∥CD的条件,并写出相应的根据.
如图,写出所有能使AB∥CD的条件,并写出相应的根据.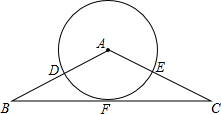 如图,在△ABC中,AB=AC,∠B=30°,⊙A与边AC、AB交于点D,E,⊙A的半径是1,若点F为BC的中点,BF=$\sqrt{3}$,求证:直线BC与⊙A相切.
如图,在△ABC中,AB=AC,∠B=30°,⊙A与边AC、AB交于点D,E,⊙A的半径是1,若点F为BC的中点,BF=$\sqrt{3}$,求证:直线BC与⊙A相切. 如图,在?ABCD中,BE⊥AC于点E,DF⊥AC于点F,又M、N分别是DC、AB的中点,求证:四边形EMFN是平行四边形.
如图,在?ABCD中,BE⊥AC于点E,DF⊥AC于点F,又M、N分别是DC、AB的中点,求证:四边形EMFN是平行四边形.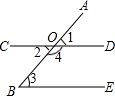 看图填理由:
看图填理由:
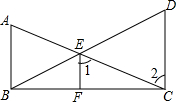 如图,已知AB⊥BC,EF⊥BC,∠1=∠2,根据推理的依据填空:
如图,已知AB⊥BC,EF⊥BC,∠1=∠2,根据推理的依据填空: