题目内容
19.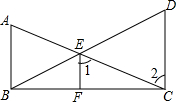 如图,已知AB⊥BC,EF⊥BC,∠1=∠2,根据推理的依据填空:
如图,已知AB⊥BC,EF⊥BC,∠1=∠2,根据推理的依据填空:∵AB⊥BC(已知)
∴∠ABC=90°(垂直的定义)
∵EF⊥BC(已知)
∴∠EFC=90°(垂直的定义)
∴∠ABC=∠EFC(等量代换)
∴EF∥AB(同位角相等,两直线平行)
∴∠1=∠2(已知)
∴EF∥CD(内错角相等,两直线平行)
∴AB∥CD(同一平面内平行于一直钱的两直线平行)
分析 利用垂直的定义可得∠ABC=∠EFC=90°,由平行线的判定定理“同位角相等,两直线平行”可得EF∥AB,再由“内错角相等,两直线平行”可得EF∥CD,易得AB∥CD.
解答 证明:∵AB⊥BC,
∴∠ABC=90°,
∵EF⊥BC,
∴∠EFC=90°,
∴∠ABC=∠EFC,
∴EF∥AB,
∵∠1=∠2,
∴EF∥CD,
∴AB∥CD.
故答案为:90°;90°;EF;AB;EF;CD;AB;CD.
点评 本题主要考查了平行线的判定,利用同一平面内平行于一直钱的两直线平行是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
9.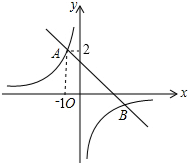 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,2),则另一个交点B的坐标为( )
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,2),则另一个交点B的坐标为( )
 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,2),则另一个交点B的坐标为( )
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,2),则另一个交点B的坐标为( )| A. | (-2,1) | B. | (2,1) | C. | (1,-2) | D. | (2,-1) |
 如图,矩形ABCD的对角线AC、BD相交于点O,AB=4,∠AOB=60°,求对角线AC的长.
如图,矩形ABCD的对角线AC、BD相交于点O,AB=4,∠AOB=60°,求对角线AC的长.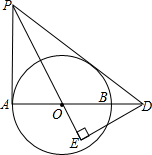 如图,在Rt△PAD中,∠PAD=90°,∠APD的角平分线PO交AD于O点,以O为圆心,OA为半径作⊙O,交AD于点B,过D作DE⊥PO交PO的延长线于点E.
如图,在Rt△PAD中,∠PAD=90°,∠APD的角平分线PO交AD于O点,以O为圆心,OA为半径作⊙O,交AD于点B,过D作DE⊥PO交PO的延长线于点E.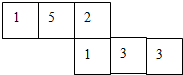 标有6个数字的立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为x,朝下一面的数字为y,得到平面直角坐标中的一个点(x,y),小敏抛掷一次立方体,则所得的点落在以坐标系原点为圆心,3为半径的圆内的概率为$\frac{1}{3}$.
标有6个数字的立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为x,朝下一面的数字为y,得到平面直角坐标中的一个点(x,y),小敏抛掷一次立方体,则所得的点落在以坐标系原点为圆心,3为半径的圆内的概率为$\frac{1}{3}$.