题目内容
2.(1)如图1,四边形ABEC是正方形,点D为△ABC内一点,且BD=AB,CD=AD,求∠CBD的度数和∠CBD与∠DBA的度数比值.(2)如图2,若把(1)中的△ABC变为一般的三角形(∠BAC≠90°,AC≠AB),但D依然是△ABC内一点,且满足∠BAC=2∠BCA,BD=AB,CD=AD,此时∠CBD与∠DBA的度数比值是否与(1)中的相同,写出你猜想的结论并加以证明.

分析 (1)作DM⊥AB,DN⊥AC垂足分别为M、N.由DM=AN=$\frac{1}{2}$AC=$\frac{1}{2}$AB推出BD=2DM,故∠DBM=30°即可解决问题.
(2)作BM∥AC,使得∠MCA=∠BAC,连接DM,先证△MCD≌△BAD得DM=DB,再由MC=MB得△DBM是等边三角形,在△ABC中利用内角和定理即可解决.
解答 解:(1)如图1,作DM⊥AB,DN⊥AC垂足分别为M、N.
∵DC=DA,DN⊥AC,
∴CN=AN=$\frac{1}{2}$AC,
∵四边形ABCD是正方形,
∴AB=AC,∠CAB=90°,∠CBA=45°,
∵∠DNA=∠NAM=∠DMA=90°,
∴四边形DNAM是矩形,
∴DM=AN=$\frac{1}{2}$AC=$\frac{1}{2}$AB,
在RT△DBM中,∵∠DMB=90°,BD=AB,
∴BD=2DM,
∴∠DBM=30°,
∴∠CBD=∠ABC-∠DBM=15°,
∴∠CBD:∠DBA=15°:30°=1:2.
(2)相同,∠CBD:∠ABD=1:2,理由如下:
如图2中,作BM∥AC,使得∠MCA=∠BAC,连接DM.
∵∠ABC≠90°,AC≠AB,
∴∠MCA+∠CAB≠180°,
∴AB与CM不平行,
∴四边形ABMC是等腰梯形,
∴CM=AB,
∵DC=DA,
∴∠DCA=∠DAC,
∴∠MCD=∠BAD,
在△MCD和△BAD中,
$\left\{\begin{array}{l}{CM=AB}\\{∠NCD=∠BAD}\\{CD=AD}\end{array}\right.$,
∴△MCD≌△BAD,
∴DM=DB,
∵∠BAC=2∠ACB=∠MCA,
∴∠MCB=∠BCA=∠MBC,
∴MB=MC,
∴BM=DM=DB,
∴△DBM是等边三角形,
∴∠MBD=60°,
∴∠ACB=∠MBC=60°-∠DBC,
∴∠BAC=2∠ACB=120°-2∠BDB,
∵∠ACB+∠BAC+∠ABC=180°,
∴60°-∠DBC+120°-2∠DBC+∠DBC+∠ABD=180°,
∴∠ABD=2∠DBC,
即∠CBD:∠ABD=1:2.
点评 本题考查正方形的性质、矩形的判定和性质、直角三角形30度角的性质、等边三角形的判定和性质等知识,通过添加辅助线构造特殊三角形是解题的关键.

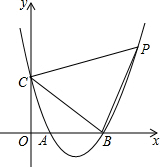 如图,抛物线y=x2-4x+3与坐标轴交于A,B,C三点,点P为对称轴右侧的抛物线上一点,若tan∠PCB=2,求P点坐标.
如图,抛物线y=x2-4x+3与坐标轴交于A,B,C三点,点P为对称轴右侧的抛物线上一点,若tan∠PCB=2,求P点坐标. 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,线段AB的端点A、B均在格点上,在正方形网格图①和图②中分别画一个三角形.
如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,线段AB的端点A、B均在格点上,在正方形网格图①和图②中分别画一个三角形. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从A开始沿折线AC→CB→BA运动,点P在AC,CB,BA边上运动的速度分别为每秒3,4,5个单位.直线l从与AC重合的位置开始,以每秒$\frac{4}{3}$个单位的速度沿CB方向平行移动,即移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P与直线l同时停止运动.当点P在BA边上运动时,作点P关于直线EF的对称点,记为点Q,若形成的四边形PEQF为菱形,则t=$\frac{6}{5}$或$\frac{30}{7}$.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从A开始沿折线AC→CB→BA运动,点P在AC,CB,BA边上运动的速度分别为每秒3,4,5个单位.直线l从与AC重合的位置开始,以每秒$\frac{4}{3}$个单位的速度沿CB方向平行移动,即移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P与直线l同时停止运动.当点P在BA边上运动时,作点P关于直线EF的对称点,记为点Q,若形成的四边形PEQF为菱形,则t=$\frac{6}{5}$或$\frac{30}{7}$.
 已知,如图,AD是△ABC的高,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,求证:AB=AC.
已知,如图,AD是△ABC的高,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,求证:AB=AC.