题目内容
9.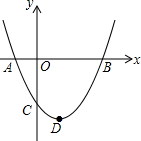 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交点C.在下面五个结论中:
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交点C.在下面五个结论中:①bc>0;②a+b+c<0;③c=-3a;④当-1<x<3时,y>0;⑤如果△ABC为直角三角形,那么仅a=$\frac{\sqrt{3}}{3}$一种情况,
其中正确的结论是①②③⑤.(只填序号)
分析 ①根据图象确定a、b、c符号即可判断.
②x=1时,y<0,由此即可判断.
③设抛物线为y=a(x+1)(x-3)=ax2-2ax-3a,由此即可判断.
④观察图象可知当-1<x<3时,y<0,故结论错误.
⑤先求出点C坐标,代入y=a(x+1)(x-3)即可解决问题.
解答 解: 由图象可知a>0,c<0,-$\frac{b}{2a}$>0,
由图象可知a>0,c<0,-$\frac{b}{2a}$>0,
∴b<0,
∴bc>0,故①正确.
∵x=1时,y<0,
∴a+b+c<0,故②正确,
∵A(-1,0),B(3,0),设抛物线为y=a(x+1)(x-3)=ax2-2ax-3a,
∴c=-3a,故③正确,
当-1<x<3时,y<0,故④错误,
∵△ABC是RT△,
∴CO2=AO•BO,
∴CO=$\sqrt{3}$,
∴点C坐标(0,-$\sqrt{3}$),代入y=a(x+1)(x-3),得到a=$\frac{\sqrt{3}}{3}$,故④正确.
故答案为①②③⑤.
点评 本题考查二次函数图象与系数关系,解题的关键是记住二次函数的性质,a>0开口向上,a<0开口向下,对称轴在y轴左侧a、b同号,对称轴在y轴右侧a、b异号,属于中考常考题型.

练习册系列答案
相关题目
20.下列二次根式中与$\sqrt{3}$是同类二次根式是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{30}$ | C. | $\sqrt{48}$ | D. | $\sqrt{54}$ |
11.将甲乙两数据进行比较,如果甲的波动性大,那么( )
| A. | 甲的标准差小 | B. | 乙的方差小 | C. | 甲的平均数大 | D. | 乙的中位数小 |
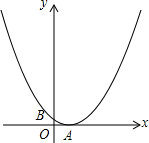 如图,抛物线经过点B(0,1),顶点A在x轴正半轴上,tan∠BAO=$\frac{1}{2}$.
如图,抛物线经过点B(0,1),顶点A在x轴正半轴上,tan∠BAO=$\frac{1}{2}$.
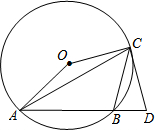 如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D.
如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D.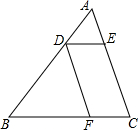 如图,在△ABC中,点D是AB边的三等分点(AD<BD),DE∥BC交AC于点E,DF∥AC交BC于点F,求$\frac{DE}{BF}$的值.
如图,在△ABC中,点D是AB边的三等分点(AD<BD),DE∥BC交AC于点E,DF∥AC交BC于点F,求$\frac{DE}{BF}$的值.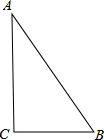 已知:如图,在Rt△ABC中,∠C=90°,AC=8,BC=6.
已知:如图,在Rt△ABC中,∠C=90°,AC=8,BC=6.