题目内容
10.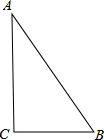 已知:如图,在Rt△ABC中,∠C=90°,AC=8,BC=6.
已知:如图,在Rt△ABC中,∠C=90°,AC=8,BC=6.(1)用尺规作出∠BAC的平分线AD,AD交BC于点D(不写作法,保留作图痕迹);
(2)在(1)所作的图中,若DE⊥AB,垂足为E.
①BD=$\frac{8}{3}$;
②求BE的长.
分析 (1)利用基本作图(作已知角的平分线)作AD平分∠BAC;
(2)如图,设BD=x,则CD=6-x,先利用勾股定理计算出在AB=10,再根据角平分线性质得到CD=DE=6-x,接着证明Rt△ADC≌Rt△ADE得到AC=AE=8,则BE=AB-AE=2,然后证明Rt△BDE∽Rt△BAC,则利用相似比可计算出BD.
解答 解:(1)如图,AD为所作;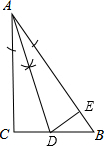
(2)如图,设BD=x,则CD=6-x,
在Rt△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∵AD平分∠BAC,DC⊥AC,DE⊥AB,
∴CD=DE=6-x,
在Rt△ADC和△ADE中,
$\left\{\begin{array}{l}{AD=AD}\\{DC=DE}\end{array}\right.$,
∴Rt△ADC≌Rt△ADE,
∴AC=AE=8,
∴BE=AB-AE=10-8=2,
∵∠DBE=∠ABC,
∴Rt△BDE∽Rt△BAC,
∴$\frac{BE}{BC}$=$\frac{BD}{AB}$,即$\frac{2}{6}$=$\frac{6-x}{10}$,解得x=$\frac{8}{3}$,
所以BD的长为$\frac{8}{3}$,BE的长为2.
故答案为$\frac{8}{3}$.
点评 本题考查了基本作图:作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线.

练习册系列答案
相关题目
15.在△ABC中,∠B=∠C,AD⊥BC于D,那么下列结论错误的是( )
| A. | AD是BC边上的中线 | B. | △ABD≌△ACD | ||
| C. | △ABC是等边三角形 | D. | AB=AC |
2. 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )
 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )| A. | ∠2与∠4是同旁内角 | B. | ∠1与∠4是内错角 | ||
| C. | ∠3与∠6是同位角 | D. | ∠2与∠5是同位角 |
19.下列说法正确的是( )
| A. | 命题可以没有题设.但一定要有结论 | |
| B. | “a的倒数是$\frac{1}{a}$”是真命题 | |
| C. | 定理一定是真命题 | |
| D. | 真命题一定是定理 |
20.下列说法正确的是( )
| A. | “黑色”和“白色”表示具有相反意义的量 | |
| B. | “快”和“慢”表示具有相反意义的量 | |
| C. | “向南100米”和“向北1000米”表示具有相反意义的量 | |
| D. | “+15米”就表示向东走了15米 |
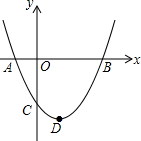 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交点C.在下面五个结论中:
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交点C.在下面五个结论中: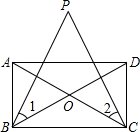 如图,矩形ABCD中,AC与BD相交于O点,∠1=∠2.求证:PB=PC.
如图,矩形ABCD中,AC与BD相交于O点,∠1=∠2.求证:PB=PC.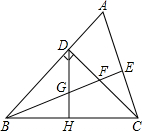 如图,在△ABC中,∠ABC=45°,BE平分∠ABC,且BE⊥AC于点E.
如图,在△ABC中,∠ABC=45°,BE平分∠ABC,且BE⊥AC于点E.