题目内容
8．某种出租车的收费标准是：起步价7元（即行驶距离不超过3km都需付7元车费），超过3km以后，每增加，加收2.4元（不足1km按1km计），某人乘这种车从甲地到乙地共支付车费19元，那么，他行程的最大值是（ ）| A． | 11km | B． | 8km | C． | 7km | D． | 5km |
分析 根据题意找出等量关系：某人乘坐这种出租车从甲地到乙地共付车费=19元．设此人从甲地到乙地的路程的最大值为xkm，由于19＞7，所以x＞3，即：某人乘坐这种出租车从甲地到乙地需付车费：7+2.4×（x-3），根据等量关系列出方程求解即可，由于不足1km按1km收费，所以此时求出的x的值即为最大值
解答 解：设此人从甲地到乙地的路程的最大值为xkm，
由题意得：（x-3）×2.4+7=19，
整理得：x-3=5，
解得：x=8．
答：此人从甲地到乙地的路程的最大值为8km．
故选B．
点评 本题考查了一元一次不等式的应用，解答本题的关键在于理解清楚题意，找出等量关系列出方程求解．
练习册系列答案
相关题目
19．
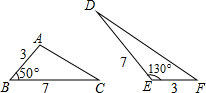如图，若△ABC和△DEF的面积分别为S1，S2，则（ ）
如图，若△ABC和△DEF的面积分别为S1，S2，则（ ）| A． | S1=$\frac{1}{2}$S2 | B． | S1=$\frac{7}{2}$S2 | C． | S1=$\frac{8}{5}$S2 | D． | S1=S2 |
16．和温带大陆性气候相比较，温带海洋性气候地区每天气温变化的幅度比较小，较适合人类居住，所以温带海洋性气候地区每天气温的（ ）比较小．
| A． | 极差 | B． | 平均数 | C． | 众数 | D． | 中位数 |
图中的AB，CD是两架靠墙摆放的梯子，AE=6米，BE=3米，DF=5米，CF=2.4米，比较哪一架梯子较陡，说明理由．
13．
如图，△ABC的顶点都在正方形网格的格点上，则cosC的值为（ ）
如图，△ABC的顶点都在正方形网格的格点上，则cosC的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{\sqrt{5}}}{5}$ | D． | $\frac{{2\sqrt{5}}}{5}$ |
20．甲、乙两人在同样的条件下比赛射击，每人打5发子弹，命中环数如下：甲：6，8，9，9，8；乙：10，7，7，7，9，则两人射击成绩稳定情况是（ ）
| A． | 甲比乙稳定 | B． | 乙比甲稳定 | C． | 甲和乙一样稳定 | D． | 无法确定 |
