题目内容
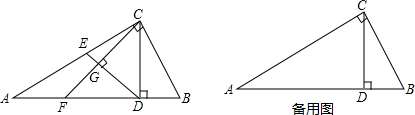
17.如图,Rt△ABC中,∠C=90°,∠A=30°,BC=2,CD是斜边AB上的高,点E为边AC上一点(点E不与点A、C重合),联结DE,作CF⊥DE,CF与边AB、线段DE分别交于点F、G;(1)求线段CD、AD的长;
(2)设CE=x,DF=y,求y关于x的函数解析式,并写出它的定义域;
(3)联结EF,当△EFG与△CDG相似时,求线段CE的长.
分析 (1)利用特殊角的三角函数可知sin∠B=$\frac{CD}{BC}$,tan∠A=$\frac{CD}{AD}$,由此求得线段CD、AD的长;
(2)证得△CDE∽△BFC,得出$\frac{CE}{BC}$=$\frac{CD}{BF}$,整理得出答案即可;
(3)分两种情况考虑:①当△EGF∽△DGC时;②当△FEG∽△CGD时;利用相似的性质探讨得出答案即可.
解答 解:(1)在Rt△BCD中,
BC=2,∠B=90°-∠A=60°,
sin∠B=$\frac{CD}{BC}$,
即CD=$\frac{\sqrt{3}}{2}$×2=$\sqrt{3}$,
同理tan∠A=$\frac{CD}{AD}$,
AD=$\frac{\sqrt{3}}{tan30°}$=3;
(2)∵∠CDE=∠BFC=90°-∠DCF,∠ECD=∠B=60°,
∴△CDE∽△BFC,
∴$\frac{CE}{BC}$=$\frac{CD}{BF}$,
即$\frac{x}{2}$=$\frac{\sqrt{3}}{y+1}$,
∴y=$\frac{2\sqrt{3}}{x}$-1,($\frac{\sqrt{3}}{2}$≤x<2$\sqrt{3}$);
(3)∠EGF=∠CGD=90°
①当△EGF∽△DGC时,∠GEF=∠GDC,
∴EF∥DC,
∴$\frac{CE}{AC}$=$\frac{DF}{AD}$,
即$\frac{x}{2\sqrt{3}}$=$\frac{y}{3}$=$\frac{\frac{2\sqrt{3}}{x}-1}{3}$,
解得x=$\frac{\sqrt{39}-\sqrt{3}}{3}$;
②当△FEG∽△CGD时,
∴∠GEF=∠GCD=∠GDF,
∴EF=DF,
又∵CF⊥DE,
∴EG=DG,
∴CD=CE=$\sqrt{3}$;
综上,CE=$\sqrt{3}$或$\frac{\sqrt{39}-\sqrt{3}}{3}$;
点评 此题考查相似的综合题,综合考查了特殊角的三角函数,相似三角形的判定与性质,注意分类讨论思想的渗透.

| A. | 11km | B. | 8km | C. | 7km | D. | 5km |
| A. | 直角 | B. | 平角 | C. | 周角 | D. | 钝角 |
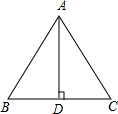 如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )
如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )| A. | ∠B=45° | B. | ∠BAC=90° | C. | BD=AC | D. | AB=AC |
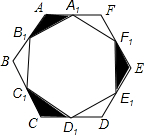 如图,已知边长为2cm的正六边形ABCDEF,点A1,B1,C1,D1,E1,F1分别为所在各边的中点,则图中阴影部分的总面积是( )
如图,已知边长为2cm的正六边形ABCDEF,点A1,B1,C1,D1,E1,F1分别为所在各边的中点,则图中阴影部分的总面积是( )| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{2\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{8}$ |
 如图所示,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为①、③、⑤(把下列正确序号填在横线上).
如图所示,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为①、③、⑤(把下列正确序号填在横线上). 小明“六一”去公园玩投掷飞镖的游戏,投中图中阴影部分有奖品(飞镖被平均分成8分).小明能获得奖品的概率是$\frac{5}{8}$.
小明“六一”去公园玩投掷飞镖的游戏,投中图中阴影部分有奖品(飞镖被平均分成8分).小明能获得奖品的概率是$\frac{5}{8}$.