题目内容
19.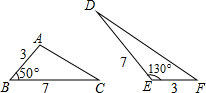 如图,若△ABC和△DEF的面积分别为S1,S2,则( )
如图,若△ABC和△DEF的面积分别为S1,S2,则( )| A. | S1=$\frac{1}{2}$S2 | B. | S1=$\frac{7}{2}$S2 | C. | S1=$\frac{8}{5}$S2 | D. | S1=S2 |
分析 作AM⊥BC于M,DN⊥EF于N,如图,在Rt△ABM中利用正弦的定义得到AM=3sin50°,利用三角形面积公式得到S1=$\frac{1}{2}$BC•AM=$\frac{21}{2}$sin50°,同样在Rt△DEN中得到DN=7sin50°,则S2=$\frac{1}{2}$EF•DN=$\frac{21}{2}$sin50°,于是可判断S1=S2.
解答 解: 作AM⊥BC于M,DN⊥EF于N,如图,
作AM⊥BC于M,DN⊥EF于N,如图,
在Rt△ABM中,∵sin∠B=$\frac{AM}{AB}$,
∴AM=3sin50°,
∴S1=$\frac{1}{2}$BC•AM=$\frac{1}{2}$×7×3sin50°=$\frac{21}{2}$sin50°,
在Rt△DEN中,∠DEN=180°-130°=50°,
∵sin∠DEN=$\frac{DN}{DE}$,
∴DN=7sin50°,
∴S2=$\frac{1}{2}$EF•DN=$\frac{1}{2}$×3×7sin50°=$\frac{21}{2}$sin50°,
∴S1=S2.
故选D.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了三角形面积公式.

练习册系列答案
相关题目
10.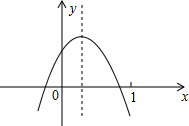 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:其中正确的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:其中正确的有( )
①a>0;c>0; ②方程ax2+bx+c=0(a≠0)有两个不等的实数根;
③y随x的增大而增大;④a-b+c<0.
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:其中正确的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:其中正确的有( )①a>0;c>0; ②方程ax2+bx+c=0(a≠0)有两个不等的实数根;
③y随x的增大而增大;④a-b+c<0.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
8.某种出租车的收费标准是:起步价7元(即行驶距离不超过3km都需付7元车费),超过3km以后,每增加,加收2.4元(不足1km按1km计),某人乘这种车从甲地到乙地共支付车费19元,那么,他行程的最大值是( )
| A. | 11km | B. | 8km | C. | 7km | D. | 5km |
9.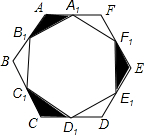 如图,已知边长为2cm的正六边形ABCDEF,点A1,B1,C1,D1,E1,F1分别为所在各边的中点,则图中阴影部分的总面积是( )
如图,已知边长为2cm的正六边形ABCDEF,点A1,B1,C1,D1,E1,F1分别为所在各边的中点,则图中阴影部分的总面积是( )
 如图,已知边长为2cm的正六边形ABCDEF,点A1,B1,C1,D1,E1,F1分别为所在各边的中点,则图中阴影部分的总面积是( )
如图,已知边长为2cm的正六边形ABCDEF,点A1,B1,C1,D1,E1,F1分别为所在各边的中点,则图中阴影部分的总面积是( )| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{2\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{8}$ |
 如图所示,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为①、③、⑤(把下列正确序号填在横线上).
如图所示,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为①、③、⑤(把下列正确序号填在横线上).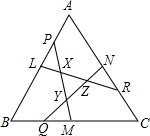 正△ABC,在边AB、BC、CA的正中间分别取点L、M、N,在边AL、BM、CN上分别取点P、Q、R,使LP=MQ=NR,当PM和RL、PM和QN、QN和RL的相交点分别是X、Y、Z时,使XY=XL,这时,△XYZ的面积是△ABC的几分之几?请写出思考过程.
正△ABC,在边AB、BC、CA的正中间分别取点L、M、N,在边AL、BM、CN上分别取点P、Q、R,使LP=MQ=NR,当PM和RL、PM和QN、QN和RL的相交点分别是X、Y、Z时,使XY=XL,这时,△XYZ的面积是△ABC的几分之几?请写出思考过程.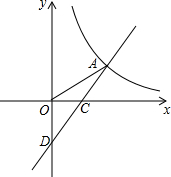 如图,在平面直角坐标系xOy中,一次函数y1=ax+b的图象与反比例函数y2=$\frac{k}{x}$的图象在第一象限内相交于点A(m,2),交x轴、y轴分别于点C、D,且C是AD的中点,S△ODA=4.
如图,在平面直角坐标系xOy中,一次函数y1=ax+b的图象与反比例函数y2=$\frac{k}{x}$的图象在第一象限内相交于点A(m,2),交x轴、y轴分别于点C、D,且C是AD的中点,S△ODA=4.