题目内容
20．甲、乙两人在同样的条件下比赛射击，每人打5发子弹，命中环数如下：甲：6，8，9，9，8；乙：10，7，7，7，9，则两人射击成绩稳定情况是（ ）| A． | 甲比乙稳定 | B． | 乙比甲稳定 | C． | 甲和乙一样稳定 | D． | 无法确定 |
分析 根据题意，分别计算甲乙两个人的方差可得，甲的方差小于乙的方差；结合方差的意义，可得甲比乙稳定．
解答 解：甲的平均数=（6+8+9+9+8）÷5=8
乙的平均数=（10+7+7+7+9）÷5=8
S甲2=$\frac{1}{5}$[（6-8）2+（8-8）2+（9-8）2+（9-8）2+（8-8）2]=1.2
S乙2=$\frac{1}{5}$[（10-8）2+（7-8）2+（7-8）2+（7-8）2+（9-8）2]=1.6
∵S甲2＜S乙2
∴甲比乙稳定．
故选：A．
点评 本题考查方差的定义与意义：一般地设n个数据，x1，x2，…xn的平均数为$\overline{x}$，则方差S2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
10．
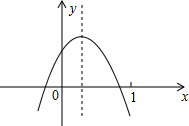已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：其中正确的有（ ）
①a＞0；c＞0； ②方程ax2+bx+c=0（a≠0）有两个不等的实数根；
③y随x的增大而增大；④a-b+c＜0．
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：其中正确的有（ ）①a＞0；c＞0； ②方程ax2+bx+c=0（a≠0）有两个不等的实数根；
③y随x的增大而增大；④a-b+c＜0．
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
8．某种出租车的收费标准是：起步价7元（即行驶距离不超过3km都需付7元车费），超过3km以后，每增加，加收2.4元（不足1km按1km计），某人乘这种车从甲地到乙地共支付车费19元，那么，他行程的最大值是（ ）
| A． | 11km | B． | 8km | C． | 7km | D． | 5km |
15．
如图，在已知的△ABC中，按以下步骤作图：
①分别以B，C为圆心，以大于$\frac{1}{2}$BC的长为半径作弧，两弧相交于两点M，N；
②作直线MN交AB于点D，连接CD．
若CD=AC，∠B=25°，则∠ACB的度数为（ ）
如图，在已知的△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于$\frac{1}{2}$BC的长为半径作弧，两弧相交于两点M，N；
②作直线MN交AB于点D，连接CD．
若CD=AC，∠B=25°，则∠ACB的度数为（ ）
| A． | 90° | B． | 95° | C． | 100° | D． | 105° |
小明“六一”去公园玩投掷飞镖的游戏，投中图中阴影部分有奖品（飞镖被平均分成8分）．小明能获得奖品的概率是$\frac{5}{8}$．
12．任意一个三角形的一组外角可以拼成一个（ ）
| A． | 直角 | B． | 平角 | C． | 周角 | D． | 钝角 |
9．
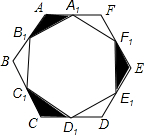如图，已知边长为2cm的正六边形ABCDEF，点A1，B1，C1，D1，E1，F1分别为所在各边的中点，则图中阴影部分的总面积是（ ）
如图，已知边长为2cm的正六边形ABCDEF，点A1，B1，C1，D1，E1，F1分别为所在各边的中点，则图中阴影部分的总面积是（ ）| A． | $\frac{3\sqrt{3}}{4}$ | B． | $\frac{2\sqrt{3}}{4}$ | C． | $\frac{\sqrt{3}}{4}$ | D． | $\frac{\sqrt{3}}{8}$ |