题目内容
7.如图①,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E.(1)四边形OCED是矩形吗?证明你的结论.
(2)如图②若AC=CD,将四边形OCED绕点O逆时针旋转,使点C落在CD边的C′处,求∠OC′C的度数.
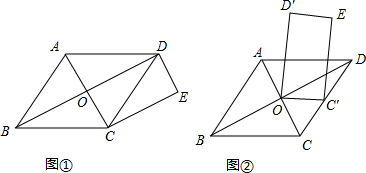
分析 (1)先判断出四边形OCED是平行四边形,再根据菱形的对角线互相垂直求出∠COD=90°,然后根据有一个角是直角的平行四边形是矩形证明;
(2)先由菱形的性质得出CD=AD,又AC=CD,那么△ACD是等边三角形,得出∠ACD=60°,再由旋转的性质得到OC=OC′,那么△OCC′是等边三角形,从而得出∠OC′C=60°.
解答 解:(1)四边形OCED是矩形,理由如下:
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是菱形,
∴∠COD=90°,
∴平行四边形OCED是矩形;
(2)在菱形ABCD中,CD=AD.
又∵AC=CD,
∴AC=CD=AD.
∴△ACD是等边三角形.
∴∠ACD=60°.
∵OC=OC′,
∴△OCC′是等边三角形.
∴∠OC′C=60°.
点评 本题考查了菱形的性质,矩形的判定,旋转的性质,是基础题,熟记性质与矩形的判定方法是解题的关键.

练习册系列答案
相关题目
19.已知x=3是关于x的方程$\frac{4}{3}$x2-2a+1=0的一个根,则a的值是( )
| A. | 5.5 | B. | 6 | C. | 6.5 | D. | 7 |
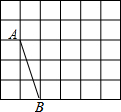 在如图所示的5×6方格中(每个方格的边长为1),点A、B在格点上.
在如图所示的5×6方格中(每个方格的边长为1),点A、B在格点上. 如图,市政府准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的余弦值为$\frac{4}{5}$,则坡面AC的长度为10m.
如图,市政府准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的余弦值为$\frac{4}{5}$,则坡面AC的长度为10m.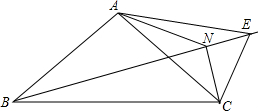 如图,在△ABC中,AB=AC,∠ABC=α.过点B作一直线l,在l上取点E,使AE=AC,连接CE.∠CAE的平分线交BE于点N,连接NC.
如图,在△ABC中,AB=AC,∠ABC=α.过点B作一直线l,在l上取点E,使AE=AC,连接CE.∠CAE的平分线交BE于点N,连接NC.