题目内容
11.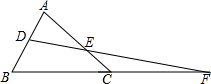 如图,D,E分别为△ABC的AB和AC上的点,且BC的延长线交DE的延长线于F点,且$\frac{DF}{EF}=\frac{AC}{AB}$,求证:DB=EC.
如图,D,E分别为△ABC的AB和AC上的点,且BC的延长线交DE的延长线于F点,且$\frac{DF}{EF}=\frac{AC}{AB}$,求证:DB=EC.
分析 作EH∥AB于H,如图,根据平行线分线段成比例定理,由EH∥BD得到$\frac{DF}{EF}$=$\frac{BD}{EH}$①,由EH∥AB得到$\frac{EC}{AC}$=$\frac{EH}{AB}$②,则利用①×②得$\frac{DF}{EF}$•$\frac{EC}{AC}$=$\frac{BD}{AB}$,加上$\frac{DF}{EF}=\frac{AC}{AB}$,则利用比例性质即可得到DB=EC.
解答 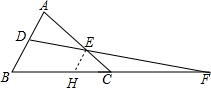 证明:作EH∥AB于H,如图,
证明:作EH∥AB于H,如图,
∵EH∥BD,
∴$\frac{DF}{EF}$=$\frac{BD}{EH}$①,
∵EH∥AB,
∴$\frac{EC}{AC}$=$\frac{EH}{AB}$②,
①×②得$\frac{DF}{EF}$•$\frac{EC}{AC}$=$\frac{BD}{AB}$,
∵$\frac{DF}{EF}=\frac{AC}{AB}$,
∴$\frac{AC}{AB}$•$\frac{EC}{AC}$=$\frac{BD}{AB}$,
∴DB=EC.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.也考查了比例的性质.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,
如图,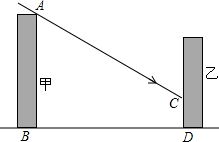 如图,在我国北方某居民区有一座甲楼,坐落在正南正北方向,楼高16米,要在甲楼的北面建一座乙楼,已知冬至这一天正午时太阳光线与水平线的夹角是32°.
如图,在我国北方某居民区有一座甲楼,坐落在正南正北方向,楼高16米,要在甲楼的北面建一座乙楼,已知冬至这一天正午时太阳光线与水平线的夹角是32°.