题目内容
6.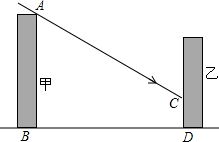 如图,在我国北方某居民区有一座甲楼,坐落在正南正北方向,楼高16米,要在甲楼的北面建一座乙楼,已知冬至这一天正午时太阳光线与水平线的夹角是32°.
如图,在我国北方某居民区有一座甲楼,坐落在正南正北方向,楼高16米,要在甲楼的北面建一座乙楼,已知冬至这一天正午时太阳光线与水平线的夹角是32°.(1)如果甲、乙两楼相距20米,求甲楼的影子落在乙楼上的部分有多高;
(2)如果甲楼的影子刚好不影响乙楼,那么两楼之间的距离应是多少米?
分析 (1)过点C作CE⊥AB于E,解直角△ACE,求出AE的长,从而求得CD的长;
(2)设射线AC交直线BD于点E.在Rt△ABE中,利用正切函数求得BE的长,即为使前后楼每层居民在冬天都能有阳光,两楼应至少相距的米数.
解答 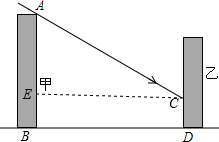 解:(1)如图,过点C作CE⊥AB于E,
解:(1)如图,过点C作CE⊥AB于E,
由题意可知∠ACE=32°,CE=BD=20m.
在Rt△ACE中,∵tan∠ACE=$\frac{AE}{CE}$,
∴AE=CE•tan∠ACE=20•tan32°≈12.5,
∴DC=EB=AB-AE=16-12.5=3.5.
答:此时南楼的影子落在北楼上约3.5米高;
(2)如图,设射线AC交直线BD于点E.
在Rt△ABE中,∵AB=16,∠E=32°,
∴BE=$\frac{AB}{tan32°}$≈25.6.
答:甲楼的影子刚好不影响乙楼,那么两楼之间的距离约是25.6米.
点评 此题考查了解直角三角形的应用,解题关键把实际问题转化为数学问题加以计算.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
16.下列计算中,正确的是( )
| A. | $\sqrt{3}$$+\sqrt{2}$=$\sqrt{5}$ | B. | 2$\sqrt{3}$+3$\sqrt{2}$=5$\sqrt{5}$ | C. | 3$\sqrt{3}$$+2\sqrt{3}$=5$\sqrt{3}$ | D. | 2$\sqrt{3}$$•4\sqrt{3}$=8$\sqrt{3}$ |
 如图,已知△ABC中,AB=AC,DE⊥AB,DF⊥AC,BG⊥AC.
如图,已知△ABC中,AB=AC,DE⊥AB,DF⊥AC,BG⊥AC.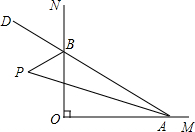 如图,已知∠MON=90°,点A、B分别是OM、ON上的动点,若P是∠BAO和∠ABO的外角∠OBD的角平分线的交点,则∠P的大小是否发生变化?为什么?
如图,已知∠MON=90°,点A、B分别是OM、ON上的动点,若P是∠BAO和∠ABO的外角∠OBD的角平分线的交点,则∠P的大小是否发生变化?为什么?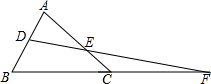 如图,D,E分别为△ABC的AB和AC上的点,且BC的延长线交DE的延长线于F点,且$\frac{DF}{EF}=\frac{AC}{AB}$,求证:DB=EC.
如图,D,E分别为△ABC的AB和AC上的点,且BC的延长线交DE的延长线于F点,且$\frac{DF}{EF}=\frac{AC}{AB}$,求证:DB=EC.