题目内容
20．《九章算术》“勾股”章中有一道题：“今有二人同所立，甲行率七，乙行率三，乙东行，甲南行十步而斜东北与乙会，问甲乙各行几何？”大意是说：已知甲、乙二人从同一地点出发，甲的速度与乙的速度之比为7：3，乙一直向东走，甲先向南走十步，后又斜向北偏东某方向走了一段后与乙相遇．这时甲、乙各走了多远？分析 设经x秒二人在B处相遇，然后利用勾股定理列出方程即可求得两人各自行了多少步．
解答 
解：设经x秒二人在B处相遇，这时乙共行AB=3x，
甲共行AC+BC=7x，
∵AC=10，
∴BC=7x-10，
又∵∠A=90°，
∴BC2=AC2+AB2，
∴（7x-10）2=102+（3x）2，
解得：x1=0（舍去），x2=3.5，
∴AB=3x=10.5，
AC+BC=7x=24.5．
答：甲行24.5步，乙行10.5步．
点评 本题考查了勾股定理的应用，解题的关键是从实际问题中抽象出直角三角形，尤其本题中的文言文更不容易理解．
练习册系列答案
相关题目
在锐角△ABC中，D、E、F分别是三条高AD、BE、CF．的垂足，连DE、EF、FD，求证：△DEC∽△AEF∽△DBF．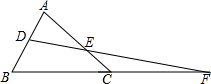
如图，D，E分别为△ABC的AB和AC上的点，且BC的延长线交DE的延长线于F点，且$\frac{DF}{EF}=\frac{AC}{AB}$，求证：DB=EC．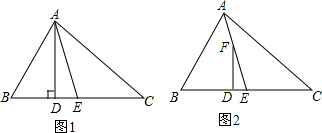
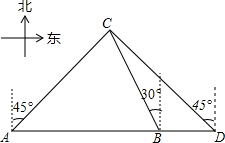如图，某轮船由西向东方向航行，在A处望见灯塔C在东北方向，航行到点B处望见灯塔C在北偏西30°方向，又航行了半小时到达D处，望见灯塔C恰好在西北方向，若轮船的速度为40海里/时，求A，B之间的距离（精确到0.1海里）．