题目内容
18. 如图,正方形ABCD中,E为对角线AC上一点,连结EB、ED,延长BE交AD于点F.
如图,正方形ABCD中,E为对角线AC上一点,连结EB、ED,延长BE交AD于点F.(1)求证:∠BEC=∠DEC;
(2)当CE=CD时,求证:DF2=FE•FB.
分析 (1)利用正方形的性质,根据SAS即可证得:△BEC≌△DEC,得出对应角相等即可;
(2)首先证明△FDE∽△FBD,根据相似三角形的对应边的比相等,即可得出结论.
解答  (1)证明:∵四边形ABCD是正方形,
(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠BCE=∠DCE,
在△BEC和△DEC中,$\left\{\begin{array}{l}{BC=DC}&{\;}\\{∠BCE=∠DCE}&{\;}\\{CE=CE}&{\;}\end{array}\right.$,
∴△BEC≌△DEC(SAS),
∴∠BEC=∠DEC.
(2)证明:连接BD,如图所示.
∵CE=CD,
∴∠DEC=∠EDC.
∵∠BEC=∠DEC,∠BEC=∠AEF,
∴∠EDC=∠AEF.
∵∠AEF+∠FED=∠EDC+∠ECD,
∴∠FED=∠ECD.
∵四边形ABCD是正方形,
∴∠ECD=$\frac{1}{2}$∠BCD=45°,∠ADB=$\frac{1}{2}$∠ADC=45°,
∴∠ECD=∠ADB.
∴∠FED=∠ADB.
又∵∠BFD是公共角,
∴△FDE∽△FBD,
∴$\frac{FE}{DF}=\frac{DF}{BF}$,
∴DF2=FE•BF.
点评 本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质;熟练掌握正方形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
8.下列图中∠1和∠2是同位角的是( )


| A. | ①、②、③ | B. | ②、③、④ | C. | ③、④、⑤ | D. | ①、②、⑤ |
9. 如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )
如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )
 如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )
如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )| A. | AB=CD | B. | AO=CO | C. | AC=BD | D. | BO=DO |
8. 如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )
如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )
 如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )
如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )| A. | 25° | B. | 35° | C. | 45° | D. | 55° |
 如图,E、F是?ABCD对角线BD上的两点,若要使四边形AECF是平行四边形.则可以添加一个条件是:BE=DF(答案不唯一);.
如图,E、F是?ABCD对角线BD上的两点,若要使四边形AECF是平行四边形.则可以添加一个条件是:BE=DF(答案不唯一);. 如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD.
如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD.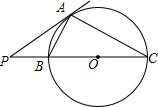 如图,PA是⊙O的切线,割线PBC与⊙O相交于点B、C,PA=6、PB=4,则BC=5.$\frac{AB}{AC}$的值为$\frac{2}{3}$.
如图,PA是⊙O的切线,割线PBC与⊙O相交于点B、C,PA=6、PB=4,则BC=5.$\frac{AB}{AC}$的值为$\frac{2}{3}$.