题目内容
8. 如图,在Rt△ACB中,∠ACB=Rt∠,D是AB的中点,tan∠ACD=$\frac{1}{3}$,求∠A,∠B的度数(精确到1′)
如图,在Rt△ACB中,∠ACB=Rt∠,D是AB的中点,tan∠ACD=$\frac{1}{3}$,求∠A,∠B的度数(精确到1′)
分析 先利用∠ACD的正切值得到∠ACD=18°24′,再根据直角三角形斜边上的中线性质得到DA=DC,则利用等腰三角形的性质得∠A=∠ACD=18°24′,然后利用互余计算∠B的度数.
解答 解:∵tan∠ACD=$\frac{1}{3}$,
∴∠ACD=18°24′,
∵D是斜边AB的中点,
∴DA=DC,
∴∠A=∠ACD=18°24′,
∴∠B=90°-∠A=90°-18°24′=71°36′.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键的灵活运用勾股定理和锐角三角函数的定义.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
19. 如图,已知AB是⊙O直径,∠D=30°,则∠AOC等于( )
如图,已知AB是⊙O直径,∠D=30°,则∠AOC等于( )
 如图,已知AB是⊙O直径,∠D=30°,则∠AOC等于( )
如图,已知AB是⊙O直径,∠D=30°,则∠AOC等于( )| A. | 155° | B. | 145° | C. | 120° | D. | 130° |
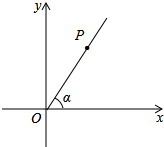 如图,点P是∠α的边OA上的一点,已知点P的横坐标为6,若sinα=$\frac{4}{5}$
如图,点P是∠α的边OA上的一点,已知点P的横坐标为6,若sinα=$\frac{4}{5}$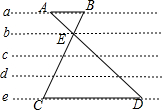 图中,a,b,c,d,e是五条等距离的平行线,线段AD和BC相交于E点(E点在直线b上).已知AB=4cm,CD=12cm,三角形ABE的面积为3cm2,三角形CDE的面积是多少平方厘米?
图中,a,b,c,d,e是五条等距离的平行线,线段AD和BC相交于E点(E点在直线b上).已知AB=4cm,CD=12cm,三角形ABE的面积为3cm2,三角形CDE的面积是多少平方厘米?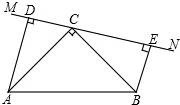 在△ABC中,∠ACB=90°,AC=BC,AD=8cm,BE=6cm,直线MN经过点C,且
在△ABC中,∠ACB=90°,AC=BC,AD=8cm,BE=6cm,直线MN经过点C,且