题目内容
20.计算:(1)$\sqrt{18}-\frac{1}{\sqrt{2}}$;
(2)$\sqrt{5}×(\sqrt{15}-\sqrt{5})$.
分析 (1)先化简,再合并同类二次根式;
(2)根据二次根式的乘法法则计算即可.
解答 解:(1)原式=3$\sqrt{2}$-$\frac{\sqrt{2}}{2}$
=$\frac{5\sqrt{2}}{2}$;
(2)原式=$\sqrt{5}$×$\sqrt{15}$-$\sqrt{5}$×$\sqrt{5}$
=5$\sqrt{3}$-5.
点评 本题考查的是二次根式的混合运算,掌握二次根式的混合运算法则是解题的关键.

练习册系列答案
相关题目
11.有大小两种圆珠笔,3枝大圆珠笔和2枝小圆珠笔的售价是14元,2枝大圆珠笔和3枝小圆珠笔的售价为11元.设大圆珠笔为x元/枝,小圆珠笔为y元/枝,根据题意,列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{3x-2y=11}\\{2x+3y=14}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{3x+2y=14}\\{2x+3y=11}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{14x-11y=3}\\{2x+3y=11}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x-2y=11}\\{2x+3y=14}\end{array}\right.$ |
8.已知$\left\{\begin{array}{l}{x=4}\\{y=-2}\end{array}\right.$是方程$\left\{\begin{array}{l}{x+y=2}\\{y-\frac{x}{2}=-4}\end{array}\right.$的解,那么一次函数y=2-x和y=$\frac{x}{2}$-4的交点坐标是( )
| A. | (4,2) | B. | (4,-2) | C. | (-4,2) | D. | (-4,-2) |
12. 如图,在四边形ABCD中,对角线AC、BD相交于O点,且AB=AD,CB=CD,则图中全等三角形共有(
如图,在四边形ABCD中,对角线AC、BD相交于O点,且AB=AD,CB=CD,则图中全等三角形共有(
 如图,在四边形ABCD中,对角线AC、BD相交于O点,且AB=AD,CB=CD,则图中全等三角形共有(
如图,在四边形ABCD中,对角线AC、BD相交于O点,且AB=AD,CB=CD,则图中全等三角形共有(| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
10.若x1、x2是一元二次方程x2-3x-6=0的两个根,则x12-2x1+x2的值是( )
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
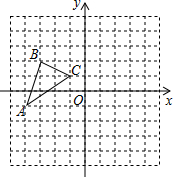 如图所示,在平面直角坐标系中,平移三角形ABC,使A的对应点A1的坐标为(1,-3),B的对应点为B1,C的对应点为C1.
如图所示,在平面直角坐标系中,平移三角形ABC,使A的对应点A1的坐标为(1,-3),B的对应点为B1,C的对应点为C1.