题目内容
4.对于给定的抛物线y=x2+ax-3,使实数p,q适合于$\frac{ap}{2}=q$-3.(1)若(p-a)2≥a2+12,求证:y=x2+px+q与x轴有交点;
(2)证明:抛物线y=-x2-px-q的最大值等于抛物线y=x2+ax-3的最小值.
分析 (1)首先对(p-a)2≥a2+12进行变形,证得p2-4q≥0即可;
(2)首先利用抛物线的性质,即可求得抛物线y=-x2-px-q的最大值和抛物线y=x2+ax-3的最小值,转化为证明整式的大小关系即可.
解答 证明:(1)∵(p-a)2≥a2+12,
∴p2-2ap+a2≥a2+12,
∴$\frac{ap}{2}$≤$\frac{{p}^{2}}{4}$-3,
∴q-3≤$\frac{{p}^{2}}{4}$-3,
∴p2-4q≥0.
∵抛物线y=x2+px+q,
令y=0,则x2+px+q=0,
∴△=p2-4q,
∴△≥0,
∴抛物线y=x2+px+q与x轴有交点;
(2)抛物线y=x2-px-q的最大值是$\frac{{p}^{2}-4q}{4}$,
抛物线y=x2+ax-3的最小值是-$\frac{{a}^{2}+12}{4}$,
∵$\frac{ap}{2}$=q-3,
∴(a-p)2=a2-4q+12,
∴(a-p)2≥0,
∴a2+p2-4q+12≥0,
∴p2-4q≥-(a2+12),
∴$\frac{{p}^{2}-4q}{4}$≥-$\frac{{a}^{2}+12}{4}$,
∴抛物线y=-x2-px-q的最大值大于等于抛物线y=x2+ax-3的最小值.
点评 本题考查了二次函数的性质以及抛物线的性质,当二次项系数a>0时,二次函数有最小值,等于定点的纵坐标;当a<0时,二次函数有最大值,等于顶点的纵坐标.

练习册系列答案
相关题目
12.下列命题不正确的是( )
| A. | 若两相等的角有一边平行,则另一边也互相平行 | |
| B. | 两条直线相交,所成的两组对顶角的平分线互相垂直 | |
| C. | 两条平行线被第三条直线所截,同旁内角的平分线互相垂直 | |
| D. | 经过直线外一点,有且只有一条直线与已知直线平行 |
9. 某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况.如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为300米,点A、D、B在同一直线上,则雪道AB的长度为( )
某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况.如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为300米,点A、D、B在同一直线上,则雪道AB的长度为( )
 某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况.如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为300米,点A、D、B在同一直线上,则雪道AB的长度为( )
某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况.如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为300米,点A、D、B在同一直线上,则雪道AB的长度为( )| A. | 300米 | B. | 150$\sqrt{2}$米 | C. | 900米 | D. | (300$\sqrt{3}$+300)米 |
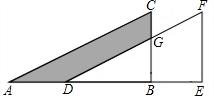 如图,将Rt△ABC沿AB方向平移得到Rt△DEF,已知BE=6,FE=10,CG=3,求阴影部分的面积.
如图,将Rt△ABC沿AB方向平移得到Rt△DEF,已知BE=6,FE=10,CG=3,求阴影部分的面积.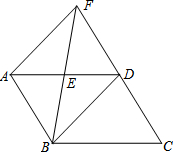 如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.
如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.