题目内容
13.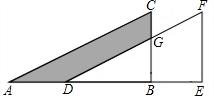 如图,将Rt△ABC沿AB方向平移得到Rt△DEF,已知BE=6,FE=10,CG=3,求阴影部分的面积.
如图,将Rt△ABC沿AB方向平移得到Rt△DEF,已知BE=6,FE=10,CG=3,求阴影部分的面积.
分析 根据平移的性质可得△DEF≌△ABC,S△DEF=S△ABC,则阴影部分的面积=梯形BEFG的面积,再根据梯形的面积公式即可得到答案.
解答 解:∵Rt△ABC沿AB的方向平移AD距离得△DEF,
∴△DEF≌△ABC,
∴EF=BC=10,S△DEF=S△ABC,
∴S△ABC-S△DBG=S△DEF-S△DBG,
∴S四边形ACGD=S梯形BEFG,
∵CG=3,
∴BG=BC-CG=10-3=7,
∴S梯形BEFG=$\frac{1}{2}$(BG+EF)•BE=$\frac{1}{2}$(7+10)×6=51.
即阴影部分的面积为51.
点评 本题考查了平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.同时考查了梯形的面积公式.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
8.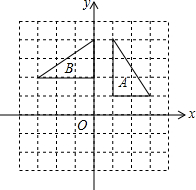 如图,在边长为1的正方形网格中,图形B是由图形A旋转得到的,则旋转中心的坐标为( )
如图,在边长为1的正方形网格中,图形B是由图形A旋转得到的,则旋转中心的坐标为( )
 如图,在边长为1的正方形网格中,图形B是由图形A旋转得到的,则旋转中心的坐标为( )
如图,在边长为1的正方形网格中,图形B是由图形A旋转得到的,则旋转中心的坐标为( )| A. | (0,1) | B. | (-1,0) | C. | (0,0) | D. | (-2,-1) |
18.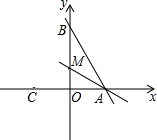 如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )
如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )
 如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )
如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )| A. | (0,4) | B. | (0,3) | C. | (-4,0) | D. | (0,-3) |
 如图,a∥b,∠1=50°,∠2=60°,则∠3=70°.
如图,a∥b,∠1=50°,∠2=60°,则∠3=70°.